Формула силы тока и его мощности: как рассчитать в электрической цепи

Электрический ток

Электричество течет по проводам. И просто «течет», почти как вода. Представьте, что вы счастливый фермер, который решил полить свой сад из шланга. Он слегка повернул кран, и вода тут же потекла по шлангу. Медленно, но не двигаясь, он бежал.

Мощность струи очень слабая. Итак, вы решили, что вам нужно больше давления, и открыли кран на полную мощность. В результате струя прорастет настолько сильно, что ни один помидор не останется без внимания, хотя в обоих случаях диаметр шланга одинаков.

Теперь представьте, что вы наполняете два ведра двумя шлангами. У зеленого давление сильнее, у желтого слабее. Ведро, наполненное водой из шланга с сильным напором, наполнится быстрее. Все дело в том, что объем воды за один и тот же период времени из двух разных шлангов тоже разный. Другими словами, количество молекул воды в зеленом шланге будет истощено гораздо больше, чем в желтом за тот же период времени.

Если взять проводник с током, произойдет то же самое: по проводнику будут двигаться заряженные частицы, как молекулы воды. Если по проводнику будет двигаться больше заряженных частиц, то и «напор» будет увеличиваться.

• Электрический ток – это направленное движение заряженных частиц.

Сила тока с точки зрения гидравлики

Я думаю, вы не раз слышали такое выражение, как «сила тока». Для чего нужна сила? Хорошо для чего? Делайте полезную или бесполезную работу. Главное что-то делать. У каждого из нас есть какая-то сила. У кого-то такая сила, что он может одним ударом разбить кирпич на куски, а другой даже соломинку поднять не может. Итак, мои дорогие читатели, электрический ток тоже имеет силу.

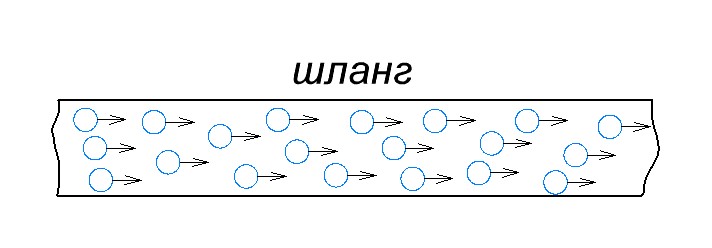
Представьте себе шланг, который вы используете для полива своего сада

Теперь проведем аналогию. Пусть шланг будет проводом, а вода в нем — электрическим током. Мы слегка открыли кран, и вода сразу же пошла по шлангу. Медленно, но не двигаясь, он бежал. Мощность струи очень слабая.

А теперь давайте откроем кран на максимум. В результате поток хлынет с такой силой, что вы даже сможете поливать соседский огород.

В обоих случаях диаметр шланга одинаков.

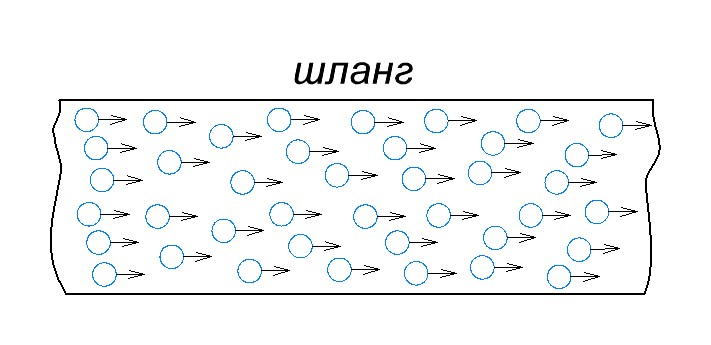
Теперь представьте, что вы наполняете ведро. При таком напоре воды, из какого шланга вы быстрее ее наполните? Конечно с зелени, где напор воды очень сильный. Но почему это происходит? Все дело в том, что объем воды за один и тот же период времени из желтого и зеленого шлангов тоже будет разным. Или, другими словами, количество молекул воды в зеленом шланге будет истощено гораздо больше, чем в желтом за тот же период времени.

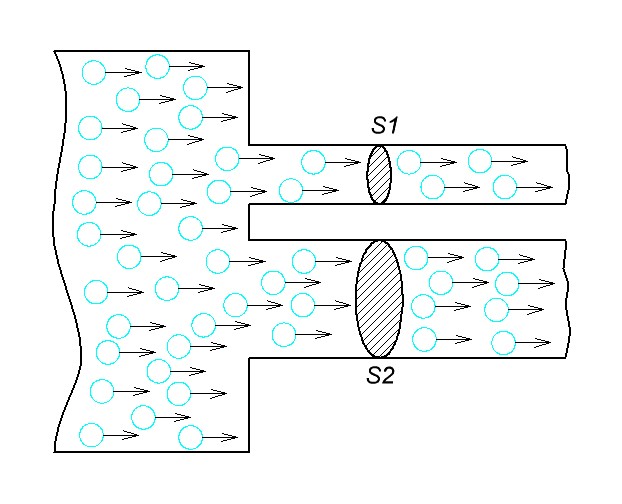
Давайте рассмотрим еще один интересный пример. Предположим, у нас есть большая труба и сварены две другие, но одна в два раза меньше другой по диаметру.

Из какой трубы выйдет больший объем воды в секунду времени? Конечно, с более толстым диаметром, потому что площадь поперечного сечения S2 большой трубы больше, чем площадь поперечного сечения S1 маленькой трубы. Следовательно, сила потока через большую трубу будет больше, чем через малую, так как объем воды, протекающей через поперечное сечение трубы S2, будет в два раза больше, чем через тонкую трубу.

Что такое сила тока?

Итак, теперь давайте применим все, что мы здесь написали о воде, к электронике. Кабель представляет собой шланг. Тонкая проволока — шланг тонкого диаметра, толстая проволока — шланг толстого диаметра, можно сказать труба. Молекулы воды – это электроны. Следовательно, толстая проволока при том же напряжении может нести больше электронов, чем тонкая. И здесь мы подходим к самой терминологии нынешней силы.

Сила тока – это количество электронов, прошедших через площадь поперечного сечения проводника в данный момент времени.

Все выглядит так. Здесь я нарисовал круглый провод, «разрезал» его и получил такое же сечение. Именно через него бегут электроны.

Возьмите 1 секунду для периода времени.

Основные единицы измерения силы тока

В качестве основной единицы измерения силы тока используется ампер (сокращенное обозначение — А). Ампер, названный в честь физика Анри Ампера, является частью Международной системы единиц (СИ).

Если через поперечное сечение за 1 секунду проходит 1 кулон электричества, то сила тока в этом проводнике равна одному амперу. Как используются вспомогательные единицы:

• миллиампер (мА), тысячная или 10-3 ампер;
• микроампер (мкА), одна миллионная или 10-6 ампер.

Сила тока – важный параметр, знание которого поможет подобрать кабели с оптимальным размером сечения для планируемой нагрузки.

Формула силы тока

Формула для чайников будет выглядеть так:

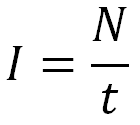
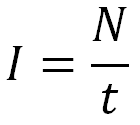
куда

I — действующая сила тока, ампер

N — количество электронов

t — период времени, за который эти электроны пройдут поперечное сечение проводника, сек

Более правильная (официальная) формула выглядит так:

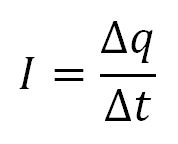
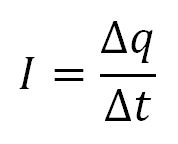
куда

Δq — заряд за определенный промежуток времени, кулон

Δt – тот же период времени, секунды

I — сила тока, ампер

В чем смысл этих двух формул? Она заключается в том, что электрон имеет заряд примерно 1,6·10-19 Кл. Следовательно, чтобы сила тока в проводе (проводнике) составляла 1 ампер, нам нужен заряд в 1 кулон = 6,24151⋅1018 электронов для прохождения поперечного сечения. 1 кулон = 1 ампер 1 секунда.

Так что теперь можно официально сказать, что если через поперечное сечение проводника за 1 секунду пролетит 6,24151⋅1018 электронов, то сила тока в таком проводнике будет равна 1 ампер! Все! Вам не нужно думать ни о чем другом! Скажи это своему учителю физики).

Если учителю не нравится ваш ответ, то скажите что-то вроде этого:

Сила тока — физическая величина, равная отношению количества заряда, прошедшего через поверхность (читай через площадь поперечного сечения) за некоторое время. Измеряется как кулон/секунда. Чтобы сэкономить время и в соответствии с другими моральными и эстетическими нормами, они согласились назвать Кулона / второго Ампера в честь французского физика.

Закон Ома

Из этой статьи вы поняли, что такое электрический ток. Но как рассчитать силу тока.

Вы увидите формулу, которая вычисляет ток для участка цепи.

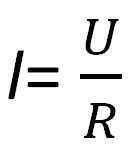
I-ток, ампер
Напряжение U, вольт
R-сопротивление, Ом

Чтобы рассчитать ток, нужно напряжение разделить на сопротивление.

Сила тока и сопротивление

Давайте еще раз посмотрим на водяной шланг и зададим себе вопросы. Что определяет расход воды? Первое, что приходит на ум, это давление. Почему молекулы воды движутся слева направо на рисунке ниже? Потому что давление слева больше, чем справа. Чем выше давление, тем быстрее вода будет бежать по шлангу, это элементарно.

Теперь вопрос: как можно увеличить количество электронов в площади поперечного сечения?

Первое, что приходит на ум, это повышение давления. При этом расход воды увеличится, но сильно вы его не увеличите, так как шланг порвется, как грелка во рту Тузика.

Второй – поставить шланг большего диаметра. В этом случае количество молекул воды через поперечное сечение пройдет больше, чем в тонком шланге:

Все те же выводы можно применить и к обычному кабелю. Чем больше его диаметр, тем больше он может «протащить» через себя ток. Чем меньше диаметр, желательно меньше нагружать, иначе он «порвется», то есть тупо сгорит. Это принцип плавких предохранителей. Внутри предохранителя находится тонкий провод. Его толщина зависит от величины тока, на которую он рассчитан.

предохранитель

Как только ток через тонкую проволоку предохранителя превышает ток, на который рассчитан предохранитель, проволока предохранителя сгорает и размыкает цепь. Ток больше не может течь через перегоревший предохранитель, так как проводка к предохранителю разомкнута.

перегоревший предохранитель

Поэтому силовые кабели, по которым «бегают» сотни и тысячи ампер, берут большого диаметра и стараются делать из меди, так как ее удельное сопротивление очень мало.

Сила тока в проводнике

Очень часто можно увидеть в физике загадки с вопросом: какая сила тока действует на проводник? Проводник, он же провод, может иметь разные параметры: диаметр, он же площадь поперечного сечения; материал, из которого изготовлена ​​проволока; длина, что тоже играет немаловажную роль.

А вообще сопротивление проводника рассчитывается по формуле:

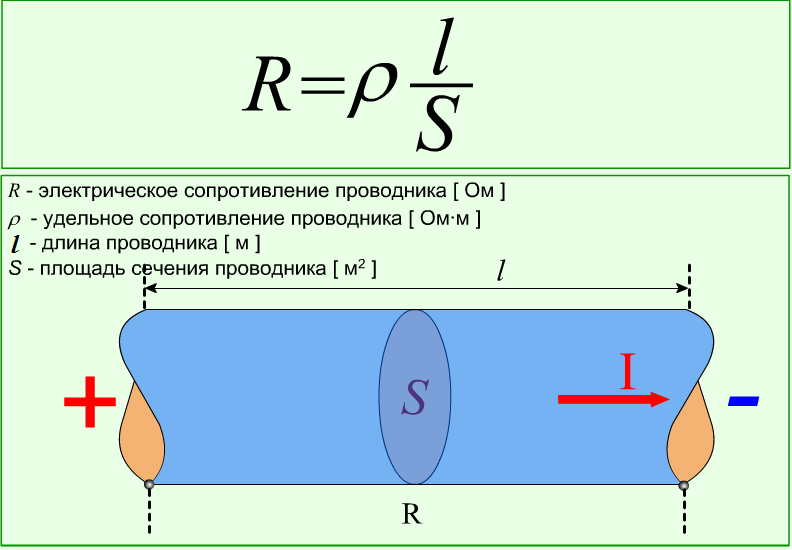
формула сопротивления проводника

Таблица с удельным сопротивлением различных материалов выглядит так.

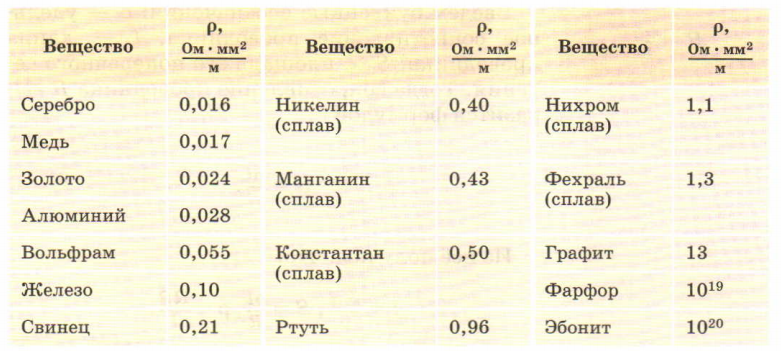
таблица сопротивлений

Чтобы найти силу тока в проводнике, мы должны использовать закон Ома для участка цепи. Выглядит ли это так:

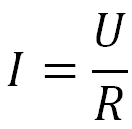
закон Ома

Домашнее задание

Имеем медный провод длиной 1 метр и площадью поперечного сечения 1 мм2. Какой ток будет течь в этом проводнике (проводе), если на его концы приложить напряжение 1 вольт?

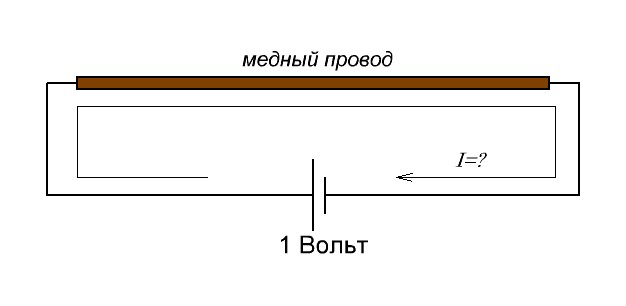
задача на силу тока в проводнике

Решение:

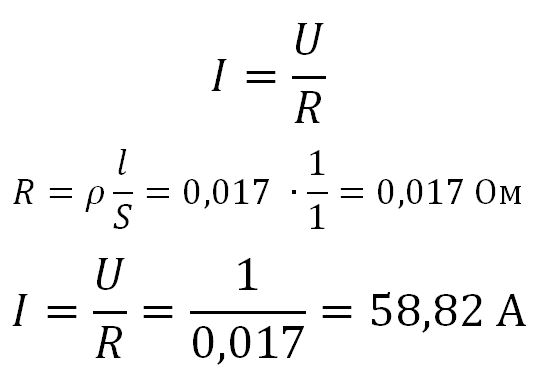
Проводники и диэлектрики

Одни делят мир на черное и белое, а мы делим его на проводники и диэлектрики.

• Проводники – это материалы, проводящие электричество. Металлы являются лучшими проводниками.
• Диэлектрики – это материалы, не проводящие электричество. Легкий!

Водители	Диэлектрики
Медь, железо, алюминий, олово, свинец, золото, серебро, хром, никель, вольфрам	Воздух, дистиллированная вода, ПВХ, янтарь, стекло, резина, полиэтилен, полипропилен, полиамид, сухая древесина, каучук

То, что диэлектрик не проводит электричество, не означает, что он не может накапливать заряд. Накопление заряда не зависит от возможности его передачи.

Направление тока

Раньше в учебниках по физике писали так: однажды решили, что ток идет от плюса к минусу, а потом узнали, что по проводам текут электроны. Но эти электроны отрицательные, а это значит, что они не могут опуститься. Но так как мы уже договорились о направлении, то оставим как есть. Вот и возник вопрос у всех: почему нельзя изменить направление тока? Но никто не получил ответа.

Сейчас пишут немного иначе: положительные частицы текут по проводнику от плюса к минусу, туда и идет ток. Здесь ни у кого нет вопросов.

Так какая версия правильная? На самом деле оба. Носители заряда в каждом типе материала разные. В металлах это электроны, в электролитах — ионы. Каждый вид частиц имеет свои признаки и необходимость бежать к полюсу противоположного заряда от источника тока. Мы не будем выбирать направление тока для каждого типа материала, чтобы решить проблему! Поэтому принято направлять ток от плюса к минусу. В большинстве задач школьного курса направление тока роли не играет, но есть то самое коварное меньшинство, где этот момент будет очень важен. Поэтому помните: мы направляем ток от большего к меньшему.

Источник тока

Вода в шланг берется из водопровода, кран с водой в земле, в общем не из ничего. Электрический ток также имеет свой источник.

В качестве источника может выступать, например, гальванический элемент (семейная батарея). Аккумулятор работает на основе химических реакций внутри него. Эти реакции высвобождают энергию, которая затем передается в электрическую цепь.

Любой источник обязательно имеет полюса: «плюс» и «минус». Полюса – это его крайние положения. По сути клеммы, к которым подключается электрическая цепь. На самом деле ток просто течет от «+» к «-».

Плотность тока

Распределение электрического тока по сечению проводника характеризуется вектором плотности тока ($bar{j}$). Где:

$$j_{n}=j cos alpha=frac{d I}{d S}(5)$

где $alpha$ — угол между векторами $bar{j}$ и $bar{n}$ ($bar{n}$ — нормаль к элементу поверхности dS), jn — проекция вектор плотности тока в направлении нормали ($bar{n}$).

Сила тока в проводнике определяется по формуле:

$$I=int_{S} jd S(6)$

где интегрирование в выражении (6) производится по всему сечению проводника S ($alpha equiv 0$)

Для постоянного тока имеем:

$I = jS (7)$

Если рассматривать два проводника с сечениями S1 и S2 и постоянными токами, то выполняется соотношение:

$$frac{j_{1}}{j_{2}}=frac{S_{2}}{S_{1}}(8)$

Как измерить силу тока?

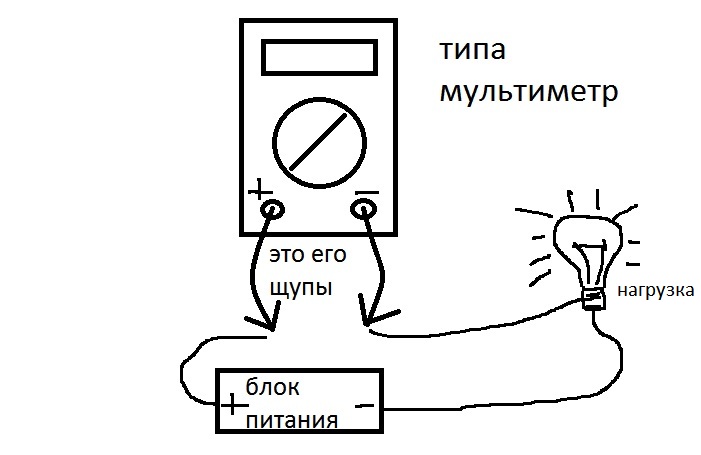
Для измерения величины тока мы должны пользоваться специальными приборами — амперметрами. В настоящее время ток можно измерить с помощью цифрового мультиметра, который может измерять ток, напряжение, сопротивление и многое другое. Чтобы измерить силу тока, мы должны таким образом вставить наш прибор в разомкнутую цепь.

Формулами

Параметры электрического тока всегда взаимосвязаны. Например, изменение значения нагрузки отображается в показателях других величин. Кроме того, эти изменения подчиняются соответствующим законам, которые выражаются через формулы. Поэтому на практике часто используют соответствующие формулы для нахождения силы тока.

Через заряд и время

Вспомните определение (рис. 1): электричеством называется величина движимого силами электрического поля заряда, превышающего условную плоскость проводника, называемую поперечным сечением проводника, в единицу времени.

Рис. 1. Определение понятия силы тока

Таким образом, если известен электрический заряд, прошедший через проводник в данное время, то нетрудно найти величину этого заряда, прошедшего в единицу времени, то есть: I = q/t

Через мощность и напряжение

В паспорте электроприбора обычно указывается его номинальная мощность и параметры электрической сети, для работы в которой он предназначен. Имея в своем распоряжении эти данные, можно рассчитать действующую силу по формуле: I = P/U.

Это выражение получено из формулы расчета мощности: P = UI.

Через напряжение или мощность и сопротивление

Сила электричества в цепи определяется законом Ома. Для этого нужно знать следующие параметры: сопротивление и напряжение на этом участке. Итак, я = U/R. Если мощность нагрузки известна, то ее можно выразить через произведение квадрата силы тока на сопротивление сечения: P = I2R, из которого

Для полной схемы это значение рассчитывается по закону Ома, но с учетом параметров источника питания.

Через ЭДС, внутреннее сопротивление и нагрузку R

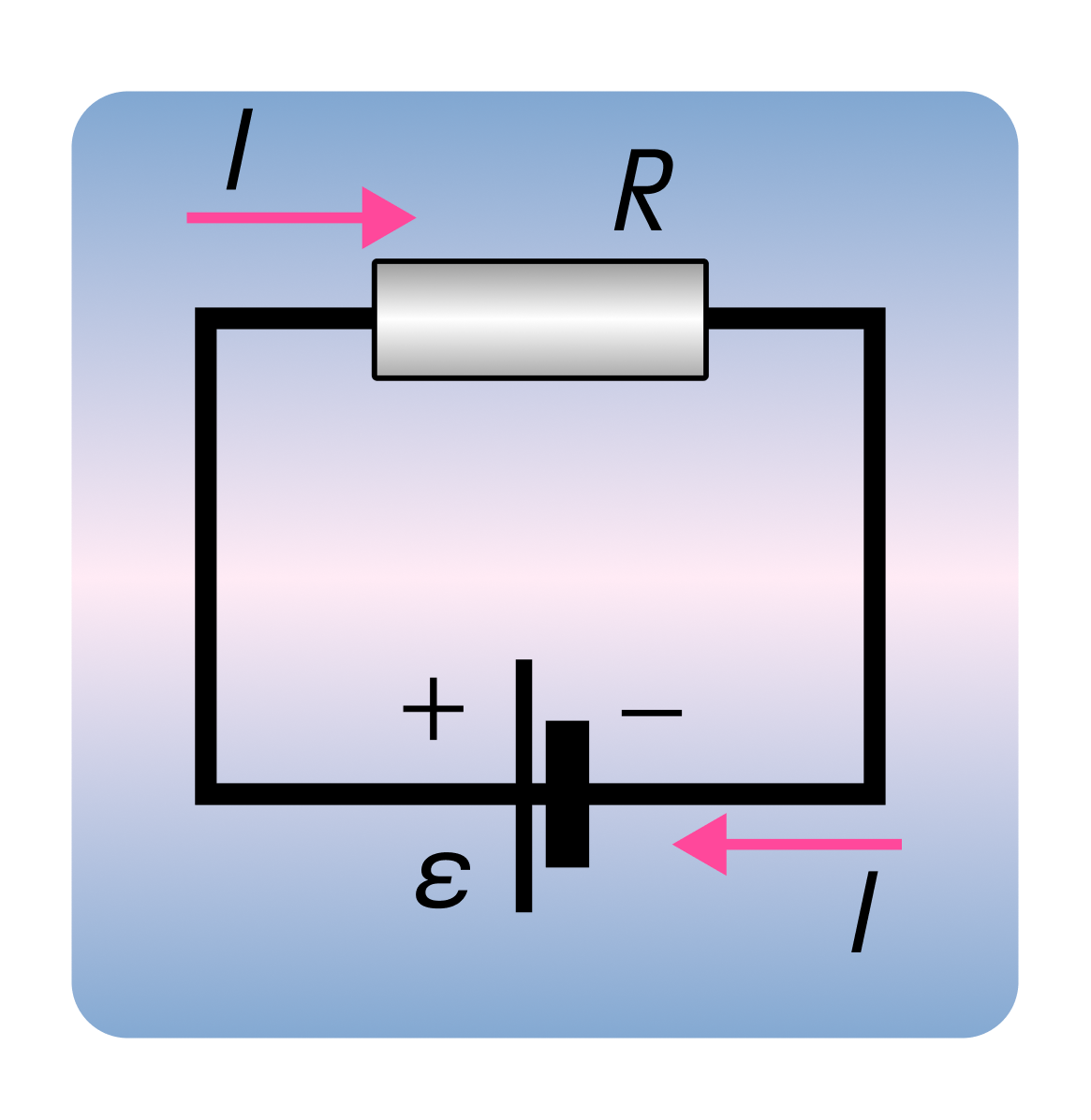
Применяя закон Ома, адаптированный ко всей цепи, максимальный ток можно рассчитать по формуле I = ε / (R+r′), если известны параметры:

• внешнее сопротивление проводников (R);
• ЭДС источника питания (ε);
• внутреннее сопротивление источника с ЭДС (r′).

Примечание! Реальные источники питания имеют внутреннее сопротивление. Так как в электрической цепи
показатель силы тока может уменьшиться из-за увеличения сопротивления источника питания или в результате падения ЭДС. Именно из-за увеличения внутреннего сопротивления аккумулятор садится и ЭДС аккумуляторов ослабевает.

Закон Джоуля-Ленца

Казалось бы, расчет силы тока по количеству тепла, выделяющегося в результате нагрева проводника, не имеет практического применения. Однако это не так. Давайте посмотрим на это на примере.

Пусть необходимо найти силу тока при работе электрочайника. Для этого вскипятите 1 кг воды и засеките время в секундах. Предположим, начальная температура была 10 ºС. Значит Q = См (τ — τ0) = 4200 Дж/кг × 1 кг (100 – 10) = 378 000 Дж.

Рис. 2. Закон Джоуля–Ленца

Из закона Джоуля-Ленца (изображение на рис. 2) следует формула:

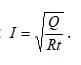
Измерив сопротивление электроприбора и подставив значения в формулу, получим величину потребляемого тока.

Измерительными приборами

Если под рукой есть измерительные приборы, то с их помощью довольно просто найти силу тока. Нужно только соблюдать правила измерения и не забывать о правилах техники безопасности.

Амперметром

При использовании приборов для измерения силы тока необходимо помнить, что в цепь они включены последовательно. Внутреннее сопротивление амперметра очень мало, поэтому прибор легко вывести из строя, если измерения проводить за пределами его расчетных значений.

Схема подключения амперметра представлена ​​на рисунке 3. Учтите, что на измеряемом участке электрической цепи должна быть нагрузка.

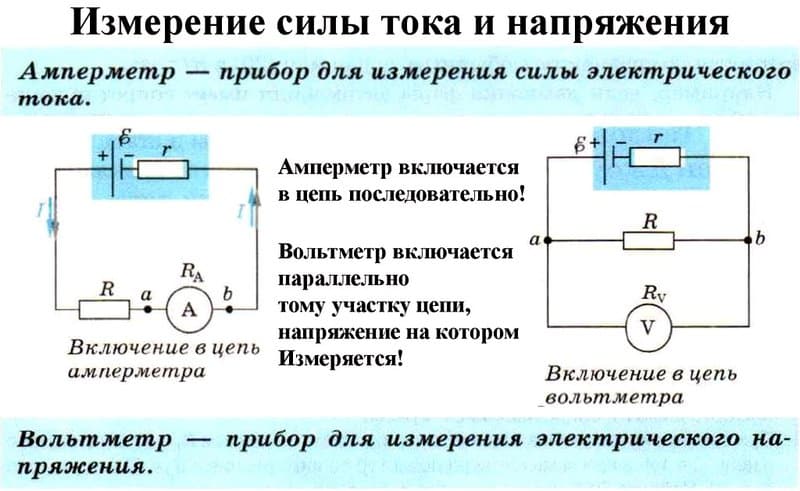
Рис. 3. Схема подключения амперметра

Большинство аналоговых амперметров, подобных показанным на рис. 4, предназначены для измерения параметров в цепях постоянного тока.

Рис. 4. Аналоговый амперметр

Обратите внимание на расположение шкалы амперметра. Цена первого деления — 50 А, а всех последующих — 10 А. Максимальное значение, которое можно измерить этим амперметром, не должно превышать 300 А. Для измерения электрических величин в меньших или больших пределах необходимы соответствующие приборы, рассчитанные на такие диапазоны его следует использовать. В этом смысле универсальность амперметра ограничена.

При измерении постоянных токов необходимо соблюдать полярность щупов при подключении амперметра. Чтобы подключить устройство, нужно разорвать цепь. Это не всегда удобно. Иногда расчет силы тока по формуле предпочтительнее, особенно если предстоит измерение в сложных электрических цепях.

Мультиметром

Преимущество мультиметра в том, что это устройство многофункционально. Современные цифровые мультиметры. Имеют режимы для измерений в цепях постоянного и переменного тока. В режиме измерения тока это измерительное устройство включается в цепь так же, как и амперметр.

Перед подключением мультиметра к цепи всегда проверяйте режим измерения и выбирайте пределы измерения, заведомо превышающие ожидаемую силу тока. После первого измерения можно перейти в режим с меньшим диапазоном.

Для работы с переменным напряжением переведите прибор в соответствующий режим. Прочтите отображаемые значения после того, как цифры перестанут мигать.

Примеры

Покажем на простых примерах, как решать задачи на расчет силы тока по формуле.

Домашнее задание 1.

На участке цепи параллельно соединены три резистора (см рис. 5). Значения сопротивления резисторов: R1 = 5 Ом; R2 = 25 Ом; R3 = 50 Ом. Требуется рассчитать силу тока для каждого резистора и для всей секции, если поддерживается постоянное напряжение 100 В.

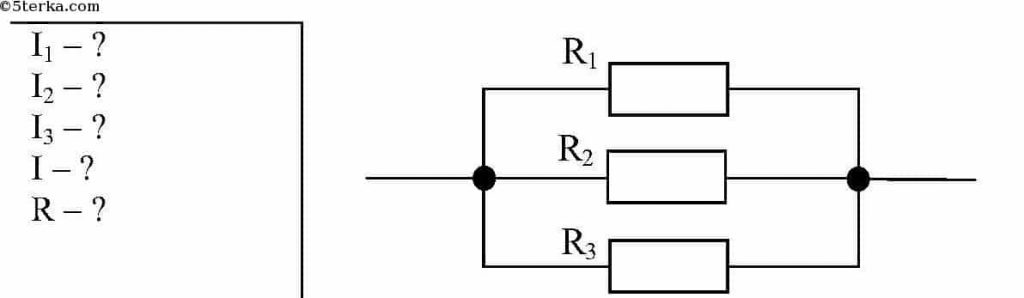
Рис. 5. Пример 1

Решение: При параллельном соединении элементов нагрузки U = постоянная, т е напряжение на всех резисторах одинаково и равно 100 В. Итак, по закону Ома I = U/R

• I1 = U/R1 = 100/5 = 20 А;
• I2 = U/R2 = 100/25 ≈ 4 А;
• I3 = U/R3 = 100/50 = 2 А.

Для расчета нужного параметра для всего участка цепи нам необходимо знать полное сопротивление этого участка. Учитывая, что при параллельном соединении элементов нагрузки в цепи их полное сопротивление равно:

Имеем: 1/R= 1/5 + 1/25 + 1/50 = 13/50; R = 50/13 ≈ 3,85 (Ом)

Итак: I = U/R = 100 В/3,85 Ом ≈26 А.

Отвечать:

• Сила тока в резисторах: I1 = 20 А; I2 = 4А; I3 = 2А
• Сила тока, подаваемого на рассматриваемый участок цепи, равна 26 А.

Задача 2.

Мощность электрочайника 2 кВт. Питается чайник от городской сети 220 В. Сколько электроэнергии потребляет этот прибор?

Решение:

Воспользуемся формулой для нахождения силы тока, включая напряжение и мощность: I = P/U.

• перевести 2 кВт в ватты: 2 кВт = 2000 Вт.
• Подставляем данные: I = 2000 Вт/220 В ≈ 9 А
• Ответ: Нагревательный элемент электрочайника рассчитан на 9А.

Задача 3.

Рассчитайте силу тока в цепи, если известно, что сопротивление 5 Ом, ЭДС источника питания 6 В, а его внутреннее сопротивление 1 Ом.

Решение.

Применяя закон Ома для полной цепи, запишем: I = ε / (R+r′)

I = 6 В / (5 Ом + 1 Ом) = 1 А.

Ответ: сила тока 1А.

Задача 4.

Сколько энергии потребляет электрическая плита за 2 часа работы, если сопротивление нагревательного элемента 40 Ом?

Решение:

За время t электричество совершит работу A = U*I*t.

Напряжение сети известно – оно равно 220 В. Силу тока находим по формуле: I = U/R, тогда A = (U2/R)*к

A = ((220В)2/40 Ом) * 2ч = 2420Втч = 2,42кВтч

Ответ: За 2 часа работы электроплита потребляет 2,42 кВтч электроэнергии.

Используя формулы расчета параметров электричества, используя фундаментальные законы физики, можно найти неизвестные данные о составных элементах электрических цепей и приборов для оценки их состояния. В каждом отдельном случае необходимо определить текущие известные параметры, которые можно использовать в последующих расчетах. Обычно это напряжение, мощность или сопротивление нагрузки.

Если можно обойтись без измерения амперметром, лучше прибегнуть к расчетам, даже если для этого требуется измерение напряжения. Такое измерение можно сделать без разрыва электрической цепи, чего нельзя сделать с помощью амперметра.

Примеры типичных токов

Текущие значения можно прочитать на информационных табличках электроприемников или в инструкциях к этим устройствам. В следующей таблице приведены типичные значения электрических токов для различных электрических рецепторов.

Потребитель	Сила тока
Электрический термометр	около 0,00001 мА
Наушники	1 мА
Лампа накаливания 60Вт	0,26 А
Лампа накаливания 75Вт	0,33 А
Холодильник	0,8 А
Зарядное устройство для смартфона (быстрая зарядка)	2А
Персональный компьютер	0,87–2,6 А
Микроволновая печь	3,5 А
Пылесос	4 — 9А
Стиральная машина	6 — 10А
Электрическая плавильная печь	15000А
Гром молния	10 000–100 000 А (в среднем 36 000 А)

Что такое мощность в электричестве: просто о сложном

Я вспомнил былину про Илью Муромца, когда он приложил все силы к соловью-вору. У бедолаги сразу в глазах посыпались искры, как пламя с картинки выше на проводке при неправильном монтаже.

Простыми словами: мощность в электричестве – это характеристическая мощность энергии, по которой оценивают как мощность генераторных установок по ее выработке, так и мощности потребителей и транспортных путей.

Все эти секции должны быть точно собраны и отрегулированы для обеспечения безопасной работы. Как только где-либо возникает неисправность, сразу развивается авария во всей цепи.

Если говорить об электрооборудовании для дома, то нужно постоянно находить баланс между:

1. устройства, подключенные к сети;
2. проводно-кабельная конструкция;
3. установка защитных устройств.

Только комплексное решение этих трех задач способно обеспечить безопасность электропроводки и жильцов.

Полная мощность и ее составляющие

Электрическая мощность (P) в физике является мерой того, насколько быстро происходит преобразование или передача электричества. Единицей измерения является ватт (Вт, Вт). Значение P зависит от напряжения (U) и тока (I) в замкнутой цепи.

Для постоянного тока, потребляемого нагрузкой, P есть произведение тока на напряжение:

Р=I*U (А*В=W).

P в цепи постоянного тока

Внимание! При этом значения обеих электрических характеристик постоянны, а значит, в каждую секунду времени их значения мгновенны.

Формула меняет вид при наличии в цепи источника электродвижущей силы Е (ЭДС):

П = И * Э.

Для цепей, где ток периодически меняет свои значения по синусоиде, эта формула не подходит. Необходимо вычислить P исходя из его мгновенных значений на временном интервале.

Суммарная мощность S по своему значению соответствует выражению:

S = U*i,

куда:

• U — разность потенциалов на зажимах, (В);
• I — ток, (А).

Единица вне системы B*A (V*A) используется для обозначения S).

Нагрузки, включаемые в цепи переменного тока, могут быть:

• активный;
• реактивный: емкостной или индуктивный.

Активная нагрузка (АН)

Аналогичную нагрузку несут элементы устройств с активным сопротивлением. Рабочая часть таких устройств нагревается при прохождении через них электричества.

Ток, проходя через нагрузку, совершает работу, затрачиваемую на нагрев, и выделяет тепловую энергию. Как измеряется этот заряд? Измеряется в омах (омах).

Примеры AN включают: утюг, электрическую плиту, катушки фена, нить накала лампы, резистивный резистор.

Довожу до вашего сведения. АН ведет себя одинаково как при постоянном, так и при переменном во времени токе.

Емкостная нагрузка

Устройства, способные накапливать энергию в электрическом поле и создавать рециркуляцию (полный или частичный возврат) энергии, называются емкостными нагрузками. Емкостная нагрузка (ЕН) при переменном напряжении, проходящем токе, меняет свою фазу на 900 вперед.

Основными элементами, связанными с HD, являются:

• конденсаторы;
• кабельные линии (емкость между жилами);
• Линии электропередачи сверхвысокого напряжения (ЛЭП;
• генераторы, работающие в режиме перевозбуждения.

EH обеспечивает реактивную мощность (Q).

Индуктивная нагрузка (ИН)

Нагрузка, в которой ток не совпадает по фазе с напряжением на 900, называется индуктивной нагрузкой. Она также потребляет Q.

При включении индуктора (дросселя), имеющего малое активное сопротивление, в сеть переменного напряжения в нем образуется ЭДС. Электродвижущая сила противодействует приложенному напряжению.

Важно! В случае чистой индуктивности L сопротивление синусоидальному току увеличивается с увеличением частоты. Средняя мощность P, рассеиваемая в такой нагрузке, равна нулю.

Примеры IN:

• асинхронные двигатели;
• электромагниты;
• дроссели;
• реакторы;
• трансформаторы;
• выпрямители

Сюда же относятся тиристорные преобразователи.

Отрицательное влияние реактивной нагрузки

Расчет мощности трехфазной сети

Если представить мощности в виде векторов, то векторы P и Q в сумме дадут общую мощность, равную:

S = √(P2 + Q2).

Формулы для P и Q:

• P = U*I*sinφ (для однофазной сети) и P = √3* U*I*sinφ (для трехфазной сети);
• Q = U*I* cosφ (для сети 220 В) и Q = √3*U*I* cosφ (для сети 380 В).

Довожу до вашего сведения. Расчеты для трехфазной сети верны для симметрично нагруженных фаз. В противном случае добавляются мощности всех фаз.

Чем меньше угол φ между векторами S и P, тем выше cosφ коэффициента мощности. Q избегает полного совпадения векторов. Нагрузка на ЛЭП и оборудование системы электроснабжения возрастает при большом значении угла. Происходит перегрев кабелей и износ оборудования энергосистемы.

На практике основными потребителями промышленных предприятий являются трансформаторы, электродвигатели и длинномерные кабели. Следовательно, лидером является ИП, потребляющая Q. Имеет место перерасход потребляемой энергии, за что компании наказываются штрафами.

Реактивная мощность (RP) имеет следующие недостатки:

• не выполняет полезную работу;
• вызывает ненужные затраты энергии и непредвиденные перегрузки электрооборудования;
• может вызвать аварийную ситуацию.

Для компенсации РМ необходимо параллельно с такими потребителями включать емкостные элементы. Для этого строят устройства компенсации Q. Они бывают конденсаторными или индуктивными, в зависимости от преобладающего вида реактивной нагрузки. Конденсаторные установки, включающие в свой состав конденсаторные батареи, размещают как в электрических подстанциях, так и в отдельных блоках. Указанная компенсация восполняет реактивную составляющую энергии, потребляемой от поставщика.

Как рассчитать электрическую мощность в быту

Формулы расчета мощности в электричестве позволяют сделать качественную оценку безопасности каждого из вышеперечисленных пунктов.

Они полностью справедливы для активной составляющей переменного тока, совершающей полезную работу. Кстати, кроме того, есть еще бесполезный — реактивный, связанный с потерями энергии. Второй раздел посвящен его описанию.

Такие расчеты удобно производить с помощью онлайн-калькулятора. Избавьтесь от рутинных математических вычислений и арифметических ошибок.

При любом из методов расчета активной мощности необходимо знать две из трех электрических величин:

1. сила тока I;
2. приложенное напряжение U;
3. сопротивление цепи r

Однофазная сеть напряжением 220 вольт

При включении в цепь активной нагрузки используют формулу: P=U*I. В случае сдвига фаз между U и I используют формулу: P=U*I*cosφ.

Трёхфазная сеть напряжением 380 В

В трехфазной сети переменного тока со сдвигом фаз результат последней формулы умножается на √3. Значение угла cosφ можно уточнить в справочнике.

Таблица cosφ для бытовой техники

При выборе сечения кабеля обычно известны суммарная мощность будущих потребителей и напряжение сети.

Нужна только сила тока, формула которой через мощность и напряжение имеет вид:

I = P/(U*cosφ).

Формула для расчета тока с использованием мощности и напряжения имеет следующие компоненты:

• P — известная мощность устройства, (Вт);
• U — напряжение питания, (220/380 В);
• cosφ — угол фазового сдвига.

Текущий расчет можно произвести с помощью онлайн-калькулятора.

Особенности расчёта в цепях переменного электричества

Для выполнения расчетов Р, потребляемых нагрузкой в ​​цепях коммутации электроэнергии, необходимо четко разделить цепи коммутации. Они могут быть монофазными и трехфазными.

В однофазных цепях Р находится путем умножения значения тока на значение напряжения (220 В). При этом учитывается наличие фазового перехода между ними.

В трехфазных сетях напряжением 380 В рассматриваются два случая:

• фазосимметричная нагрузка;
• асимметричная фазовая нагрузка.

В первом случае Р находится по формуле:

P = √3*U*I* cosφ.

Во втором случае необходимо вычислить P для каждой фазы (A, B, C). Общее значение P является результатом суммы:

Всего P = PfA + PfB + PfS.

Внимание! Когда необходимо найти полную мощность трехфазной цепи, значения реактивной добротности находят по тому же принципу.

Рассчитать ток по мощности можно, зная какое напряжение: фазное (220 В) или линейное (380 В), также и в этом случае выражая его из общей формулы Р.

Как измерить электрическую мощность дома

Существует и другая возможность оценки активной мощности — измерение ее в цепи тока специальными приборами — ваттметрами.

Промышленный лабораторный ваттметр может обеспечить точные измерения. Изготавливается как устройство, работающее с аналоговыми сигналами, помимо использования цифровых технологий.

В домашней электропроводке точные расчеты не нужны. Для этого доступны различные типы более простых ваттметров.

Популярны устройства, которые можно включить в розетку и подключить к шнуру питания потребителя, включить их и тут же снять показания на дисплее в ваттах.

Называются они так: розетка ваттметра. Они измеряют чисто активную мощность переменного тока.

Такие устройства не позволяют электрику выполнять сложные операции под напряжением, когда необходимо измерить:

• рабочее напряжение;
• сила тока;
• фазовый угол между векторами тока и напряжения.

Затем все данные требуется дополнительно ввести в формулу расчета мощности по току и напряжению, и по ней производятся расчеты.

Этот метод можно упростить, внимательно наблюдая за показаниями электросчетчика индукционной системы с вращающимся диском. Рассмотрим совершенную работу: мощность, потребляемую в течение заданного времени.

Однако скорость вращения диска характеризует только величину потребления. Вам просто нужно рассчитать, сколько раз он делает оборот в минуту, и перевести его в ватты на основе паспортной таблички, расположенной на коробке.

Мощность тока через резистор

Пусть переменный ток
течет через резистор
. Напряжение на резисторе, как известно, колеблется синфазно с током:

Следовательно, для мгновенной мощности получаем:

(два)

Мы видим, что мощность не все время отрицательна: резистор забирает энергию из цепи, но не возвращает ее в цепь.

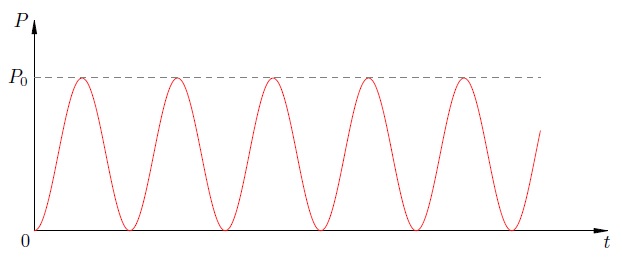
Питание переменного тока через резистор.

Максимальное значение
наша мощность связана с амплитудами тока и напряжения обычными формулами:

На практике, однако, интерес представляет не максимальная, а средняя текущая мощность. Это понятно. Возьмем, к примеру, обычную лампочку, которая включена у вас дома. По нему течет ток с частотой
Гц т.е в секунду
колебания тока и напряжения. Понятно, что в течение достаточно длительного времени в лампочке выделяется средняя мощность, величина которой находится где-то между
а также
. Где именно?

Еще раз внимательно посмотрите на рис 1. Есть ли у вас интуитивное ощущение, что средняя мощность соответствует «середине» нашей синусоиды, а значит, принимает значение
?

Это мнение абсолютно правильное! Как оно есть. Конечно, можно дать математически строгое определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу гипотезу прямым вычислением, но нам это не нужно. Достаточно интуитивного понимания простого и важного факта:

среднее значение квадрата синуса (или косинуса) за период равно
.

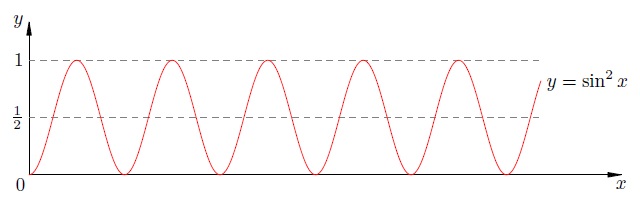
Среднее значение квадрата синуса равно

Итак, для среднего
текущая мощность на резисторе имеем:

(3)

В связи с этими формулами вводятся так называемые эффективные (или действующие) значения напряжения и тока (фактически это не что иное, как значения среднеквадратичного напряжения и мы это уже видели : среднеквадратичная скорость молекул идеального газа (лист «Уравнение состояния идеального газа»):

(4)

Формулы (3), записанные через действующие значения, полностью аналогичны соответствующим формулам для постоянного тока:

Так что если берете лампочку, то сначала подключите ее к источнику постоянного напряжения
, а затем к источнику переменного напряжения с тем же действующим значением
, то в обоих случаях лампочка будет гореть с одинаковой интенсивностью.

Эффективные значения (4) чрезвычайно важны для практики. Получается, что вольтметры и амперметры переменного тока показывают именно действующие значения (так они устроены). Также известно, что пресловутый
outlet Volts – это действующее значение напряжения бытовой электросети.

Мощность тока через конденсатор

Пусть конденсатор заряжается
. Как известно, ток через конденсатор опережает фазное напряжение на
:

Для мгновенной мощности получаем:

График зависимости мгновенной мощности от времени.

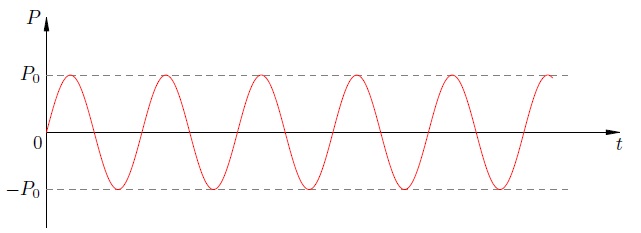
Питание переменного тока через конденсатор.

Каково среднее значение мощности? Он соответствует «середине» синусоиды и в данном случае равен нулю! Мы видим это сейчас как математический факт. Но было бы интересно с физической точки зрения понять, почему мощность тока через конденсатор равна нулю.

Для этого построим графики напряжения и тока в конденсаторе за один период колебаний.

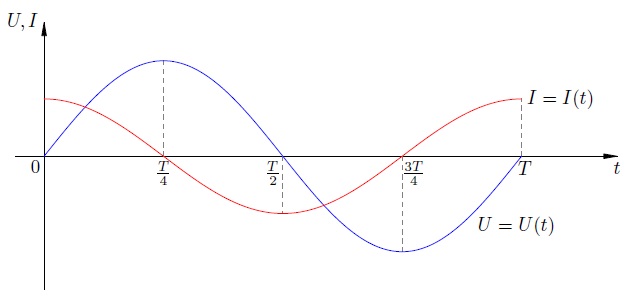
Напряжение на конденсаторе и ток через него.

Рассмотрим четыре четверти периода по очереди.

1. Первый триместр,
. Напряжение положительное и увеличивается. Ток положительный (течет в положительном направлении), конденсатор заряжается. По мере увеличения заряда конденсатора ток уменьшается.

Мгновенная мощность положительна: конденсатор накапливает энергию, поступающую из внешней цепи. Эта энергия возникает за счет работы внешнего электрического поля, продвигающего заряды на конденсаторе.

2. Второй триместр,
. Напряжение все еще положительное, но оно уменьшается. Ток меняется на противоположный и становится отрицательным: конденсатор разряжается против направления внешнего электрического поля, в конце второй четверти конденсатор полностью разряжается.

Мгновенная мощность отрицательна: конденсатор выделяет энергию. Эта энергия возвращается в цепь: она идет на работу против электрического поля внешней цепи (конденсатор, так сказать, «толкает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигаться).

3. Третий квартал,
. Внешнее электрическое поле меняет направление: напряжение становится отрицательным и увеличивается по абсолютной величине. Сила тока отрицательна: конденсатор заряжается в отрицательном направлении.

Ситуация полностью аналогична первому триместру, только знаки напряжения и тока противоположны. Мощность положительная: конденсатор снова накапливает энергию.

4 четвертая четверть,
. Напряжение отрицательное и модуль уменьшается. Конденсатор разряжается против внешнего поля: сила тока положительна.

Мощность отрицательна: конденсатор возвращает энергию в цепь. Ситуация аналогична второму триместру, опять же с заменой знаков тока и напряжения на противоположные.

Мы видим, что энергия, взятая конденсатором из внешней цепи в течение первой четверти периода колебаний, полностью возвращается в цепь в течение второй четверти. Затем этот процесс повторяется снова и снова. Именно поэтому средняя мощность, потребляемая конденсатором, оказывается равной нулю.

Мощность тока через катушку

Пусть к катушке приложено переменное напряжение
. Ток через катушку не совпадает по фазе с напряжением
:

Для мгновенной мощности получаем:

Опять же, средняя мощность оказывается равной нулю. Причины этого, в общем-то, те же, что и в случае с конденсатором. Рассмотрим графики изменения напряжения и тока через катушку за период (рис. 5).

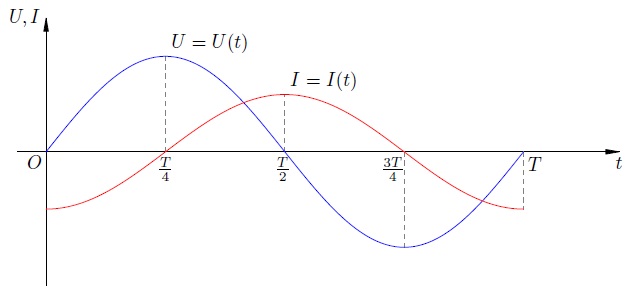
Напряжение на катушке и ток через нее.

Мы видим, что в течение второй и четвертой четверти периода энергия поступает в катушку из внешней цепи. В самом деле, напряжение и сила тока имеют одинаковые знаки, сила тока возрастает по абсолютной величине; Для создания тока внешнее электрическое поле совершает работу против электрического поля вихря, и эта работа увеличивает энергию магнитного поля катушки.

В первой и третьей четвертях периода напряжение и ток имеют разные знаки: катушка возвращает энергию в цепь. Электрическое поле вихря, поддерживающее убывающий ток, перемещает заряды против внешнего электрического поля и тем самым совершает положительную работу. И зачем эта работа? За счет энергии, ранее накопленной в катушке.

Таким образом, энергия, накопленная в катушке в течение одной четверти периода, полностью возвращается в цепь в течение следующей четверти. Следовательно, средняя мощность, потребляемая катушкой, оказывается равной нулю.

Мощность тока на произвольном участке

Рассмотрим теперь более общий случай. Пусть есть произвольный участок цепи: он может содержать резисторы, конденсаторы, катушки… К этому участку приложено переменное напряжение
.

Как мы знаем из предыдущего листа «Переменный ток. 2″, на этом участке имеется некоторый фазовый сдвиг между напряжением и током
. Пишем так:

Итак, для мгновенной мощности имеем:

(пять)

Теперь мы хотели бы определить, какова средняя мощность. Для этого преобразуем выражение (5) по формуле:

В результате получаем:

(6)

Но среднее значение количества
равен нулю! Следовательно, средняя мощность равна:

(7)

Эту формулу можно записать, используя действующие значения (4) напряжения и тока:

Формула (7) охватывает все три рассмотренные выше ситуации. В случае резистора имеем
, и мы приходим к формуле (3). Для конденсатора и катушки
, а средняя мощность равна нулю.

Кроме того, формула (7) дает представление об очень общей задаче, связанной с передачей электроэнергии. Чрезвычайно важно, чтобы
потребитель находился как можно ближе к агрегату. В противном случае потребитель начнет возвращать в сеть значительную часть энергии (что ему невыгодно), и, кроме того, возвращаемая энергия будет безнадежно расходоваться на нагревательные кабели и другие элементы цепи.

С этой проблемой приходится сталкиваться разработчикам электрических схем, содержащих электродвигатели. Обмотки электродвигателя имеют большие индуктивности и возникает ситуация, близкая к «чистой» катушке. Во избежание бесполезной циркуляции энергии по сети в схему включают дополнительные фазосдвигающие элементы, например, так называемые компенсационные конденсаторы.