Что такое контур электрической цепи: из чего состоит колебательный

Общие сведения

Колебательный контур — это электрическая цепь, состоящая из конденсатора и катушки индуктивности, которая используется для генерации свободных электромагнитных колебаний в радиопередатчиках и приемниках. Это устройство используется в качестве различных фильтров (полосовых и режекторных). Для настройки сигналов в сторону увеличения или уменьшения амплитуды используется этот элемент радиуса. Основная функция схемы — частотная фильтрация.

Устройство получило широкое применение в военной сфере. Фильтры шумоподавления используются в радиолокационных станциях. Противник использует различные глушилки, блокирующие обнаружение цели. В состав оборудования входит специальное устройство, состоящее из обычной схемы, но с сердечником из специального сплава. Помехи «отфильтровываются» и оператор РЛС получает полную картину воздушной обстановки.

Устройство также может быть использовано для автоматизации. Например, самолеты включают в себя блок управления частотой. Основными его элементами являются два контура, настроенные всего на две частоты – 760 и 840 Гц, которые получают напряжение частотой 790 Гц от специального генератора. Последний излучает всего 395 Гц.Если частота отклоняется ниже номинального значения, то уменьшается реактивное сопротивление одного из контуров.

После этого срабатывает электроника блока и выдается сигнал на увеличение оборотов генератора. Когда значение частоты превышает номинальное значение, реактивное сопротивление другой цепи увеличивается. В результате этого срабатывает автоматика и поступает другой вид сигнала на снижение скорости генератора.

Виды и особенности

Различают два типа колебательных контуров: последовательные и параллельные. Они отличаются типом соединения емкостных и индуктивных элементов. В первом случае они соединены последовательно, а во втором – параллельно. Для его работы требуется постоянная электрическая энергия, иначе она затухает, так как часть ее расходуется на создание электромагнитного поля и нагрев провода обмотки индуктора. Цепь также может быть разомкнутой и замкнутой. Вскрытие происходит без специального защитного кожуха.

При решении задач по физике можно встретить интересное понятие — идеальный колебательный контур. Если в задании встречается такое слагаемое, это говорит о том, что энергия остается в системе и не идет на процессы, описанные выше.

Устройство постоянно генерирует электромагнитные колебания, то есть это как вечный двигатель, но такого быть не может вовсе. На практике при расчете параметров учитывают затухание — постепенное уменьшение амплитуды электромагнитной волны.

Последовательное соединение

Последовательная схема представляет собой простейшую резонансно-колебательную систему. Он состоит из двух элементов, соединенных последовательно. Через них при подключении переменного напряжения будет протекать ток переменной составляющей. Его значение определяется законом Ома: i = U/Zlc. В этой формуле Zlc представляет собой сумму реактивных сопротивлений катушки индуктивности (Xl) и конденсатора (Xc).

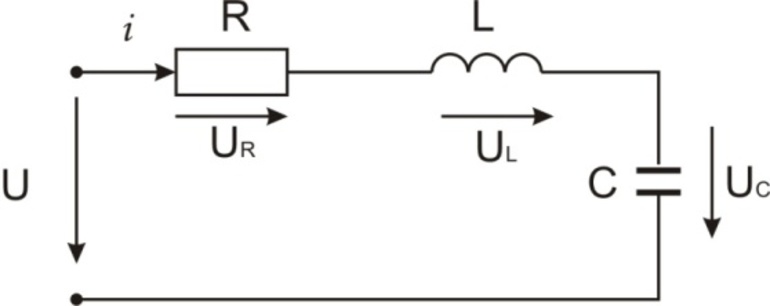
Количества определяются по формулам Xl = wL и Xc = 1/(wC). Параметр w — это угловая частота, которую можно найти из этой зависимости через частоту переменного тока и число Pi: w = 2 * Pi * f. Из соотношений можно сделать вывод, что реактивное сопротивление у индуктивности увеличивается с увеличением f, а у емкости уменьшается. В первом случае вид зависимости называют прямопропорциональным, а во втором — обратнопропорциональным.

При определенном значении частоты сопротивления двух элементов равны по абсолютной величине друг другу. Поэтому это явление называется резонансом колебательной системы. Частота w при этом условии называется собственной резонансной частотой контура. Вычислить его достаточно просто, так как для получения уравнения необходимо приравнять две формулы: wL = 1/(wC). Далее вам нужно выразить значение f: f = (1 / (L * C))^(½) / 2Pi. Последнее соотношение называется формулой Томсона.

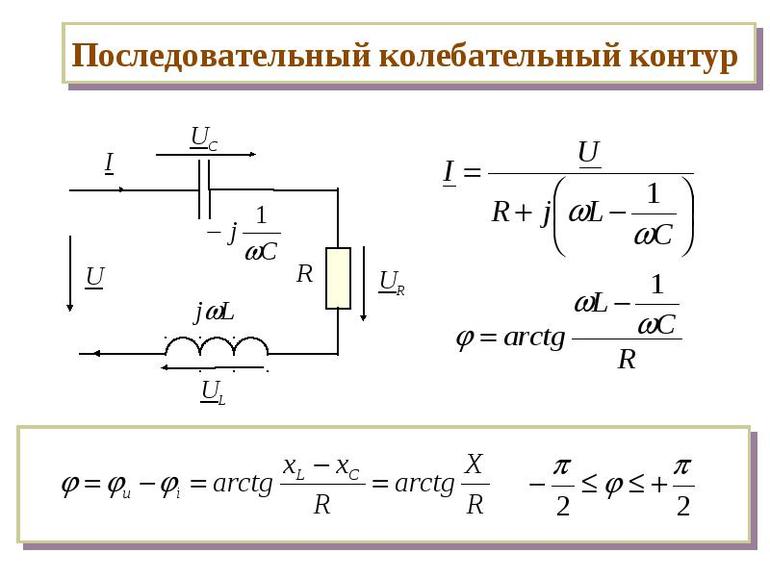
При подключении цепи к цепи (источнику) генерации переменного напряжения с активным сопротивлением R полное сопротивление цепи (Z) определяют по соотношению Z = R2 + Zlc2^(½). Если возникает резонанс, то Z = R и реактивная составляющая исчезает.

Схема имеет две наиболее важные характеристики: добротность (Q) и волновое сопротивление (p). Последнее является значением сопротивления реактивного типа при резонансе. Он рассчитывается по формуле p = (L*C)^(½) и показывает, сколько энергии от катушки и конденсатора накоплено. Для емкости величина определяется отношением Wc = (C * U2)/2, а для индуктивности — Wl = (L * I2)/2.

Связь между количеством энергии, запасенной конденсатором и катушкой, и показателем потерь называется добротностью колебательного контура (Q). Параметр определяет амплитуду и ширину резонансной частотной характеристики и показывает превышение запаса энергии над потерями в колебании. При этом учитывается реактивная нагрузка R. Характеристика определяется по формуле Q=(1/R)*(L/C)^(½).

В некоторых случаях добротность может быть описана другим тождеством: Q = p/R. Современные приборы выполнены в виде дискретных катушек, и их добротность варьируется от нескольких единиц до сотен. Системы, построенные по принципу пьезоэлектронных устройств (кварцевых резонаторов), имеют высокий показатель добротности, значение которого может достигать 1 тыс и более. Потери в контуре (d) — это характеристика, обратная добротности. Он определяется следующим соотношением: d = 1/Q.

Параллельный контур

Цепь параллельного типа также состоит из конденсатора и катушки. Отличие в том, что эти два элемента соединены параллельно друг с другом. Этот тип устройства используется чаще, чем последовательная схема. Для нахождения полного сопротивления индуктивного характера нельзя просто сложить значения Xl и Xc. Добавляются только проводимости двух элементов.

Из курса физики известно, что проводимость обратно пропорциональна сопротивлению, т е. Xc = 1/Gc и Xl = 1/Gl. Поэтому формулы для параллельного подключения выглядят так:

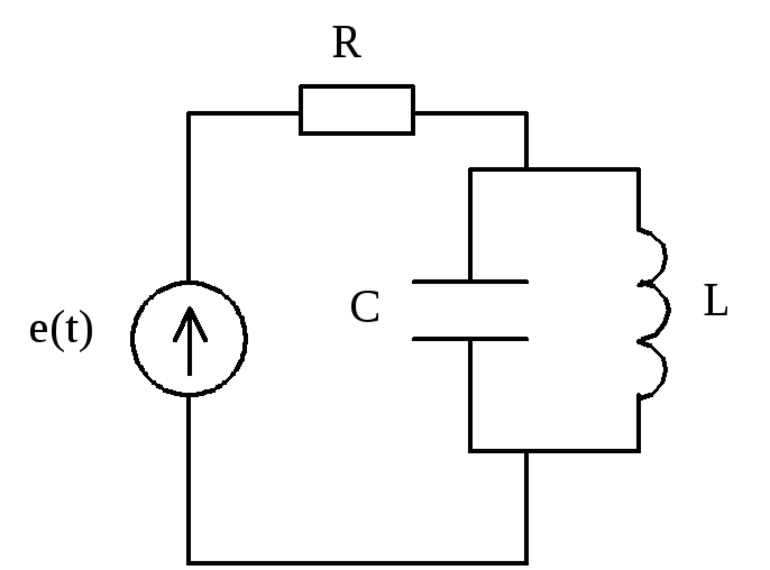
1. Gл = 1/мкл.
2. GC=wC.
3. Q = R * (C / L)^(½).

Например, рассмотрим электрическую цепь, состоящую из генератора переменного тока и параллельной цепи. В какой-то момент их частоты совпадут. Кроме того, проводимости двух элементов равны по абсолютной величине друг другу. В результате возникает явление токового резонанса.

В цепи будет только активное сопротивление Рекв, которое в радиотехнике называется эквивалентом. Он рассчитывается по формуле Req = Q * p. Если частота не соответствует резонансной, то в устройстве происходят другие процессы: на низких частотах наблюдается уменьшение индуктивного сопротивления, а на высоких частотах — емкостного сопротивления.

При работе схемы за период колебаний дважды происходит обмен энергией между катушкой и конденсатором. В радиоэлементе течет ток, который в Q раз сильнее внешнего.

Колебательный контур LC

Колебательный контур

— электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.

Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.

— Конденсатор С

— реактивный элемент. Он обладает способностью накапливать и высвобождать электрическую энергию. — индуктор
Л
— реактивный элемент. Он обладает способностью накапливать и высвобождать магнитную энергию.

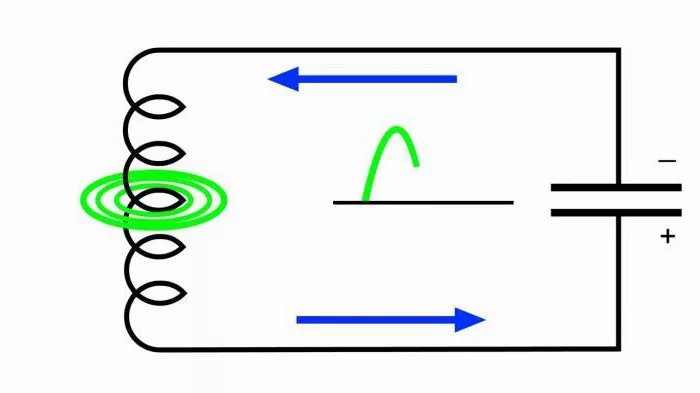
Рассмотрим, как возникают и поддерживаются свободные электрические колебания в параллельном LC-контуре

Основные свойства индуктивности

— Ток, протекающий в индукторе, создает магнитное поле с энергией. — Изменение тока в катушке вызывает изменение магнитного потока в ее витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.

Природа электромагнитных колебаний в контуре

Период свободных колебаний LC-контура

можно описать следующим образом:

Если конденсатор C

заряжен до напряжения
Ты
, потенциальная энергия его заряда будет. Если катушку индуктивности подключить параллельно заряженному конденсатору
Л
, ток разряда конденсатора будет протекать по цепи, создавая в катушке магнитное поле.

Внешний магнитный поток будет создавать ЭДС противоположного направления току в катушке, что будет препятствовать нарастанию тока с каждым витком, поэтому конденсатор будет разряжаться не мгновенно, а через время t

1, которая определяется индуктивностью катушки и емкостью конденсатора из расчета
ты
1 = . По прошествии времени
ты
1, когда конденсатор разряжается до нуля, ток в катушке и магнитная энергия будут максимальными. Магнитная энергия, накопленная катушкой в ​​это время, будет. В идеальном рассмотрении при полном отсутствии потерь в цепи
Европа
будет равно
НАШИ
. Таким образом, электрическая энергия конденсатора будет преобразована в магнитную энергию катушки.

Кроме того, изменение (уменьшение максимума) магнитного потока накопленной энергии катушки создаст в ней ЭДС, которая продолжит ток в том же направлении и запустит процесс заряда конденсатора током индукции. Уменьшение от максимума до нуля в момент времени t

2 =
ты
1, зарядит конденсатор от нуля до максимального отрицательного значения (
-Т
). Тогда магнитная энергия катушки будет преобразована в электрическую энергию конденсатора.

Описанные интервалы t

1 и
ты
2 будет составлять половину полного периода колебаний в цепи. Во второй половине процессы аналогичны, только конденсатор разрядится от отрицательного значения и направление тока и магнитного потока изменится. Магнитная энергия будет накапливаться в катушке с течением времени
ты
3 изменение полярности полюсов.

На заключительном этапе колебаний (t

4), накопленная магнитная энергия катушки зарядит конденсатор до его первоначального значения
Ты
(при отсутствии потерь) и процесс колебаний будет повторяться.

Действительно, при наличии энергетических потерь на активном сопротивлении проводников, фазных и магнитных потерь колебания будут затухать по амплитуде. Время т

1 +
ты
2 +
ты
3 +
ты
4 будет периодом колебаний. Частота свободных колебаний контура ƒ = 1 /
Т
Частота свободных колебаний – это резонансная частота цепи, в которой реактивное сопротивление индуктивности XL=2πfL

равно реактивному сопротивлению емкости
ХС=1/(2πfС)
.

Расчёт частоты резонанса LC-контура:

Предлагается простой онлайн-калькулятор для расчета резонансной частоты колебательного контура.

Необходимо ввести значения и кликнуть мышкой в ​​таблице. При изменении множителей результат автоматически пересчитывается.

Верхняя

Расчёт частоты:

Резонансная частота LC-колебательного контура f = 1/(2π√(LC))

Расчёт ёмкости:

Емкость LC-колебательного контура C = 1/(4𲃲L)

Расчёт индуктивности:

Индуктивность LC-резонансного контура L = 1/(4𲃲C)

Как работает контур колебаний

Работа колебательного контура основана на циклическом преобразовании энергии индуктивности в качественный показатель КПД конденсатора и наоборот. Предположим, что конденсатор полностью заряжен и запасенная в нем энергия максимальна. При подключении к индуктору он начинает разряжаться. При этом через индуктивность начинает протекать ток, вызывающий появление ЭДС самоиндукции, призванной уменьшить протекающий ток. Это означает, что начинается процесс перезарядки конденсатора. В тот момент, когда энергия устройства становится равной нулю, это же значение для катушки максимально.

Также энергия индуктивности уменьшается и расходуется на зарядку емкости с противоположной полярностью. После уменьшения коэффициента самоиндукции до нуля он снова имеет максимальное значение на конденсаторе.

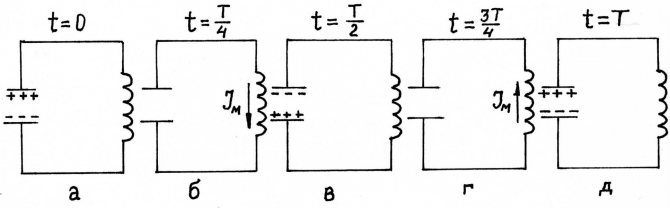
Процессы в системе

Важно! В идеале этот процесс может продолжаться бесконечно. В реальных устройствах колебание затухает со скоростью, пропорциональной потерям в цепи возбуждения.

Независимо от количества энергии, наличия потерь, частота колебаний постоянна и зависит только от значений параметров коэффициента самоиндукции и емкости. Эта величина называется резонансной. Формула резонанса учитывает величину емкости и индуктивности колебательного контура.

Осциллограмма

При воздействии на электрическую цепь с катушкой внешнего сигнала с частотой, равной резонансной, резко возрастает амплитуда изменения положения частиц. Резонанс отсутствует, когда частоты не совпадают. Из-за предельных значений электрическую цепь с индуктором часто называют резонансной.

Потери в цепи с индуктором (потери в диэлектрике конденсатора, сопротивлении самого прибора, соединительных проводов) ограничивают величину предельных изменений направления движения частиц. Вследствие этого введена характеристика электрической цепи, называемая добротностью. Коэффициент качества обратно пропорционален предельному значению потерь.

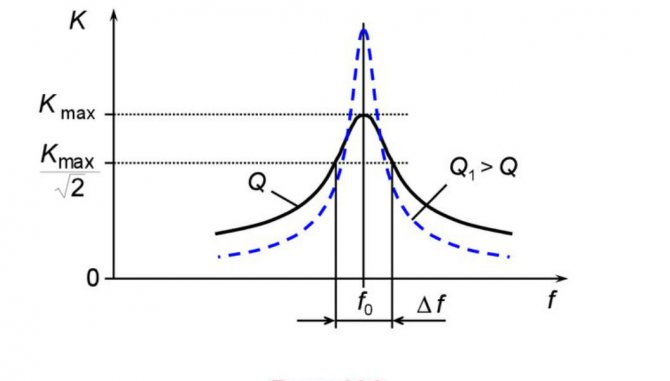
Зависимость предельной частоты от добротности

Важно! Уменьшение добротности приводит к тому, что предел изменений направления происходит не только на основной частоте, но и на некотором приближении к ней, то есть в определенной полосе частот, где резонансное значение находится на уровне средних, Средняя. Чем выше коэффициент качества, тем уже становится полоса пропускания.

Энергетические превращения в колебательном контуре

Продолжаем рассматривать незатухающие колебания в цепи, считая сопротивление катушки нулевым. Конденсатор имеет емкость
, индуктивность катушки
.

Поскольку потери тепла отсутствуют, энергия не уходит из цепи: она постоянно перераспределяется между конденсатором и катушкой.

Возьмем момент, когда заряд на конденсаторе максимален и равен
а тока нет. Энергия магнитного поля катушки в этот момент равна нулю вся энергия
схема концентрируется на конденсаторе:

Теперь, наоборот, рассмотрим момент, когда ток максимален и равен
и конденсатор разряжается. Энергия конденсатора равна нулю. Вся энергия цепи запасается в катушке:

В произвольный момент времени, когда заряд на конденсаторе
и по катушке течет ток
, энергия цепи равна:

В этом случае,

(а)

Соотношение (1) используется для решения многих задач.

Электромеханические аналогии

В предыдущем руководстве по самоиндукции мы отметили аналогию между индуктивностью и массой. Теперь мы можем установить еще несколько соответствий между электродинамическими и механическими величинами.

Для пружинного маятника имеем соотношение, аналогичное (1):

(два)

Здесь, как вы уже поняли,
— жесткость пружины
масса маятника,
а также
— текущие значения координаты и скорости маятника,
а также
являются его высшими значениями.

Сравнивая между собой равенства (1) и (2), видим следующие соответствия:

(3)

(4)

(пять)

(6)

На основе этих электромеханических аналогий можно представить формулу для периода электромагнитных колебаний в колебательном контуре.

Действительно, период колебаний пружинного маятника, как известно, равен:

В соответствии с аналогиями (5) и (6) здесь заменяем массу
для индуктивности
, а жесткость
для возврата депозита
. Мы получаем:

(7)

Электромеханические аналогии не подводят: формула (7) дает правильное выражение для периода колебаний в колебательном контуре. Она называется формулой Томсона. Вскоре мы представим его наиболее строгий вывод.

Гармонический закон колебаний в контуре

Помните, что колебания называются гармониками, если колебательная величина изменяется во времени по закону синусов или косинусов. Если вам удалось забыть эти вещи, обязательно повторите лист «Механические колебания».

Колебания заряда на конденсаторе и силы тока в цепи оказываются гармониками. Мы попробуем это сейчас. Но прежде надо установить правила выбора знака заряда конденсатора и силы тока; ведь при колебаниях эти величины будут принимать как положительные, так и отрицательные значения.

Сначала мы выбираем положительное направление для обхода контура. Выбор роли не играет; сделать это против часовой стрелки (рис. 10).

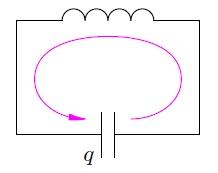
Рис. 10. Положительное направление байпаса

Сила тока считается положительной
.

Заряд конденсатора
— это заряд того, что на вашей пластине, на которую течет положительный ток (то есть на пластине, на которую указывает стрелка направления шунта). В этом случае
— заряд на левой стороне конденсатора.

При таком выборе знаков тока и заряда справедливо соотношение:
(при другом выборе знаков могло получиться
). Действительно, знаки обеих частей одинаковы: если
левая пластина увеличивается, а значит
а также
меняется со временем, но энергия цепи остается неизменной:

(8)

Следовательно, производная энергии по времени равна нулю:
. Возьмем производную по времени от обеих частей соотношения (8); не забывайте, что сложные функции остаются дифференцированными (если
— функция
, то по правилу дифференцирования сложной функции производная квадрата нашей функции будет равна:
):

Подставляя здесь
а также
, мы получаем:

Но сила тока не тождественно нулевая функция; поэтому

Давайте перепишем это как:

(9)

Мы получили дифференциальное уравнение для гармонических колебаний вида
, куда
. Это доказывает, что заряд конденсатора колеблется по гармоническому закону (то есть по закону синусов или косинусов). Циклическая частота этих колебаний равна:

(10)

Это значение также называют собственной частотой контура; именно с этой частотой в цепи происходят свободные (или, как говорят, собственные) колебания. Период колебаний равен:

Мы снова приходим к формуле Томсона.

Гармоническая зависимость нагрузки от времени в общем случае имеет вид:

(11)

Циклическая частота
находится по формуле (10); амплитуда
и начальная фаза
определяются из начальных условий.

Мы подробно рассмотрим ситуацию, обсуждавшуюся в начале этой брошюры
заряд конденсатора максимален и равен
(как на рис. 1); тока в петле нет. Итак, начальная фаза
, так что заряд меняется по закону косинусов с амплитудой
:

(12)

Найдем закон изменения силы тока. Для этого продифференцируем соотношение (12) по времени, опять же не забывая о правиле нахождения производной комплексной функции:

Мы видим, что сила тока также изменяется по гармоническому закону, на этот раз по закону синуса:

(13)

Амплитуда силы тока равна:

Наличие «минуса» в действующем законе изменения (13) понять несложно. Возьмем, к примеру, интервал времени
(Фигура 2).

Ток течет в отрицательном направлении:
. Насколько
, фаза колебания приходится на первую четверть:
. Грудь в первом триместре положительна; следовательно, синус в (13) будет положительным на рассматриваемом интервале времени. Поэтому для обеспечения отрицательности тока знак минус в формуле (13) действительно необходим).

Теперь посмотрите на рис. 8. Ток течет в положительном направлении. Как в этом случае работает наш «минус»? Узнайте, что здесь происходит!

Представим графики колебаний нагрузки и тока, то есть графики функций (12) и (13). Для наглядности приведем эти графики на одних и тех же координатных осях (рис. 11).

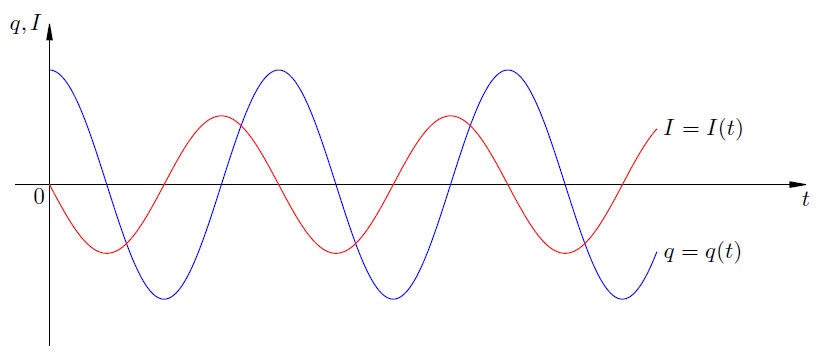
Рис. 11. Графики нагрузки и колебаний тока

Обратите внимание, что нули нагрузки возникают при текущих максимумах или минимумах; и наоборот, текущие нули соответствуют максимумам или минимумам нагрузки.

Используя формулу распределения

запишем текущий закон изменения (13) в виде:

Сравнивая это выражение с законом изменения заряда
, видим, что фаза тока, равная
, плюс фаза нагрузки
на сумму
. В этом случае говорят, что ток приводит заряд в движение по фазе
.

Зарядный ток опережает по фазе на
графически проявляется в том, что текущий график смещается влево на
что касается программы зарядки. Интенсивность тока достигает, например, своего максимума за четверть периода до того, как нагрузка достигает своего максимума (и четверть периода соответствует только разности фаз
).

Вынужденные электромагнитные колебания

Как вы помните, в системе возникают вынужденные колебания под действием периодической движущей силы. Частота вынужденных колебаний совпадает с частотой движущей силы.

Вынужденные электромагнитные колебания будут совершаться в цепи, подключенной к источнику синусоидального напряжения (рис. 12).

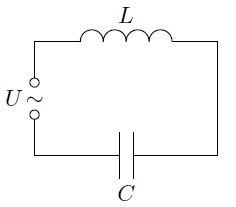
Рис. 12. Вынужденные колебания

Если напряжение источника изменяется по закону:

то колебания нагрузки и тока происходят в цепи с циклической частотой
(и с точкой соответственно
). Источник переменного напряжения как бы «навязывает» контуру свою частоту колебаний, заставляя его забыть о собственной частоте
.

Амплитуда вынужденных колебаний заряда и тока зависит от частоты
: амплитуда тем больше, чем ближе
на собственной частоте цепи
.На
возникает резонанс – резкое увеличение амплитуды колебаний. Мы обсудим резонанс более подробно в следующей брошюре о переменном токе.

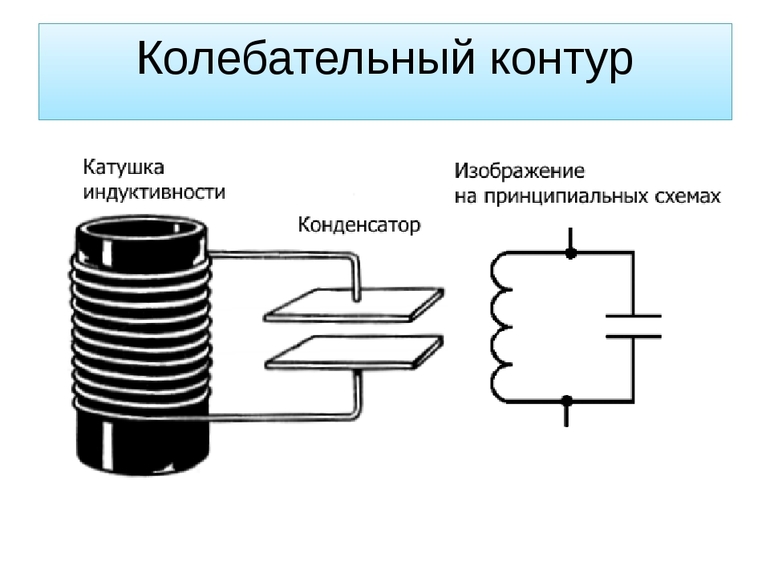
Из чего он состоит?

Колебательный контур состоит из катушки и конденсатора. Он может содержать резистор (элемент с переменным сопротивлением). Индуктор (или соленоид) представляет собой стержень, на который намотаны несколько слоев обмотки из медной проволоки. Этот элемент создает колебания в колебательном контуре. Стержень, расположенный посередине, называется дросселем или сердечником.

Катушка колебательного контура колеблется только при наличии накопленного заряда. Когда через него проходит ток, он создает заряд, который затем излучается в цепь, если напряжение падает. Провода катушки обычно имеют очень небольшое сопротивление, которое всегда остается постоянным. В цепи колебательного контура очень часто происходит изменение напряжения и тока. Это изменение подчиняется определенным математическим законам:

• U = U0*cos(w*(t-t0) , где U — напряжение в данный момент времени t, U0 — напряжение в момент времени t0, w — частота электромагнитных колебаний.

Еще одним неотъемлемым компонентом схемы является электрический конденсатор. Это элемент, состоящий из двух пластин, которые разделены диэлектриком. В этом случае толщина слоя между пластинами меньше их размеров. Такая конструкция позволяет накапливать на диэлектрике электрический заряд, который затем может быть передан в цепь.

Отличие конденсатора от батареи в том, что происходит не превращение веществ под действием электрического тока, а прямое накопление заряда в электрическом поле. Таким образом, с помощью конденсатора можно накопить достаточно большой заряд, который можно отдать сразу. При этом сила тока в цепи значительно возрастает.

Кроме того, колебательный контур состоит еще из одного элемента — резистора. Этот элемент имеет сопротивление и предназначен для контроля тока и напряжения в цепи. Если сопротивление резистора увеличить при постоянном напряжении, сила тока уменьшится по закону Ома:

• I = U/R, где I — ток, U — напряжение, R — сопротивление.

Катушка индуктивности

Давайте подробнее рассмотрим все тонкости работы катушки индуктивности и лучше поймем ее роль в колебательном контуре. Как мы уже говорили, сопротивление этого элемента стремится к нулю. Поэтому при подключении к цепи постоянного тока может произойти короткое замыкание. Однако, если вы подключите катушку к цепи переменного тока, она работает нормально. Это позволяет сделать вывод, что элемент оказывает сопротивление переменному току.

Но почему это происходит и как возникает сопротивление при переменном токе? Чтобы ответить на этот вопрос, мы должны прибегнуть к такому явлению, как самоиндукция. При прохождении тока через катушку возникает электродвижущая сила (ЭДС), которая создает препятствие для изменения тока. Величина этой силы зависит от двух факторов: индуктивности катушки и производной силы тока по времени. Математически эта зависимость выражается уравнением:

• E = -L​​* I'(t) , где E — значение ЭДС, L — значение индуктивности катушки (она разная для каждой катушки и зависит от количества витков катушки обмотки и их толщины), I'(t) — производная силы тока по времени (скорость изменения силы тока).

Сила постоянного тока не меняется со временем, поэтому при его воздействии сопротивление отсутствует.

А вот при переменном токе все его параметры постоянно изменяются по закону синуса или косинуса, в результате чего возникает ЭДС, препятствующая этим изменениям. Такое сопротивление называется индуктивным и рассчитывается по формуле:

• XL = w*L, где w — частота колебаний контура, L — индуктивность катушки.

Интенсивность тока в соленоиде увеличивается и уменьшается линейно по нескольким законам. Это означает, что если вы перестанете подавать ток на катушку, она еще какое-то время будет заряжать цепь. А если при этом резко прервать подачу тока, произойдет разряд из-за того, что заряд попытается распределиться сам и покинуть катушку. Это серьезная проблема промышленного производства. Такой эффект (хотя и не относящийся полностью к колебательному контуру) можно наблюдать, например, при вынимании вилки из розетки. При этом проскакивает искра, которая в таких масштабах не может навредить человеку. Это связано с тем, что магнитное поле не исчезает сразу, а постепенно рассеивается, индуцируя токи в других проводниках.

Катушка является основой того, из чего состоит колебательный контур. Индуктивности последовательно включенных соленоидов складываются. Далее мы подробно рассмотрим все тонкости строения этого элемента.

Что такое индуктивность?

Индуктивность катушки колебательного контура — это единичный показатель, численно равный электродвижущей силе (в вольтах), которая возникает в контуре при изменении тока на 1 А за 1 секунду. Если соленоид подключен к цепи постоянного тока, то его индуктивность описывает энергию магнитного поля, которое создает этот ток, по формуле:

• W=(L*I2)/2, где W — энергия магнитного поля.

Коэффициент индуктивности зависит от многих факторов: геометрии соленоида, магнитных характеристик сердечника, количества витков провода. Еще одним свойством этого индикатора является то, что он всегда положителен, потому что переменные, от которых он зависит, не могут быть отрицательными.

Индуктивность также можно определить как свойство проводника с током накапливать энергию в магнитном поле. Измеряется в Генри (назван в честь американского ученого Джозефа Генри).

Электрический конденсатор

Емкость колебательного контура определяется емкостью электрического конденсатора. О его внешнем виде было написано выше. Теперь разберем физику процессов, которые в нем происходят.

Поскольку пластины конденсатора состоят из проводника, по ним может протекать электрический ток. Однако между двумя пластинами имеется препятствие: диэлектрик (это может быть воздух, дерево или другой высокоомный материал. Поскольку заряд не может перейти с одного конца провода на другой, он накапливается на обкладках конденсатора. Это увеличивает мощность магнитного и электрического полей вокруг него.Таким образом, когда заряд прекращается, все электричество, накопленное на пластинах, начинает передаваться в цепь.

Каждый конденсатор имеет номинальное напряжение, оптимальное для его работы. Если этот элемент эксплуатируется длительное время при напряжении выше номинального, срок его службы значительно сокращается. На конденсатор колебательного контура постоянно воздействуют токи, а потому при его выборе нужно быть очень внимательным.

Кроме обычных конденсаторов, о которых шла речь, есть еще ионисторы. Это более сложный элемент — его можно описать как нечто среднее между аккумулятором и конденсатором. Диэлектриком в ионисторах, как правило, служат органические вещества, между которыми находится электролит. Вместе они создают двойной электрический слой, что позволяет хранить в такой конструкции во много раз больше энергии, чем в традиционном конденсаторе.

Что такое ёмкость конденсатора?

Емкость конденсатора – это отношение заряда конденсатора к напряжению, при котором он находится. Это значение можно рассчитать очень просто, используя математическую формулу:

• C = (e0 * S)/d, где e0 — диэлектрическая проницаемость диэлектрического материала (табличное значение), S — площадь обкладок конденсатора, d — расстояние между обкладками.

Зависимость емкости конденсатора от расстояния между обкладками объясняется явлением электростатической индукции: чем меньше расстояние между обкладками, тем сильнее они влияют друг на друга (по закону Кулона), тем больше заряд обкладки пластин и тем ниже напряжение. А с уменьшением напряжения значение емкости увеличивается, так как ее также можно описать следующей формулой:

• C = q/U, где q — заряд в кулонах.

Стоит поговорить о единицах измерения этой величины. Емкость измеряется в фарадах. 1 фарад — это достаточно большое значение, чтобы существующие конденсаторы (но не ионисторы) имели емкость, измеряемую в пикофарадах (триллион фарад).

Резистор

Ток в колебательном контуре также зависит от сопротивления контура. И кроме двух описанных элементов, составляющих колебательный контур (катушки, конденсаторы), есть еще и третий — резистор. Он отвечает за создание сопротивления. Сопротивление отличается от других элементов тем, что имеет высокое сопротивление, которое на некоторых моделях можно изменить. В колебательном контуре он выполняет функцию регулятора мощности магнитного поля. Вы можете соединить несколько резисторов последовательно или параллельно, тем самым увеличивая сопротивление цепи.

Сопротивление этого элемента также зависит от температуры, поэтому нужно быть осторожным при его работе в цепи, так как при прохождении тока он нагревается.

Сопротивление резистора измеряется в омах и его значение можно рассчитать по формуле:

• R = (p*l)/S, где p — удельное сопротивление материала резистора (измеряется в (Ом*мм2)/м); l — длина резистора (в метрах); S – площадь поперечного сечения (в квадратных миллиметрах).

Как связать параметры контура?

Вот мы и подошли к физике работы колебательного контура. С течением времени заряд на обкладках конденсатора изменяется по дифференциальному уравнению второго порядка.

Если решить это уравнение, то получится несколько интересных формул, описывающих процессы, происходящие в цепи. Например, циклическая частота может быть выражена через емкость и индуктивность.

Однако самой простой формулой, позволяющей вычислить многие неизвестные величины, является формула Томсона (названная в честь английского физика Уильяма Томсона, выведшего ее в 1853 году):

• T = 2 * n * (L * C) 1 / 2.T — период электромагнитных колебаний, L и C — соответственно индуктивность катушки колебательного контура и емкость элементов контура, n — ИП номер.

Расстройка устройства

Расстройка – это настройка контура на частоту, отличную от резонансной. Последнее возникает при совпадении частотных характеристик радиодетали и генератора. На некоторых устройствах этого следует избегать. Для получения резонанса необходимо использовать один из трех способов изменения характеристик:

• частота генератора;
• индуктивность;
• контейнеры

Последние два метода можно делать одновременно для достижения наилучшего эффекта. Расстройки делятся на три типа: абсолютные, обобщенные и относительные. Во-первых, это разница между частотами контура и резонанса. Обобщенный рассчитывается с использованием отношения реактивного сопротивления к активному сопротивлению. Относительная выражается как отношение абсолютной расстройки к резонансной частоте.

Также расстройка бывает положительной и отрицательной. В первом случае необходимо, чтобы частота генератора была больше частоты контура. Для отрицательного должно выполняться еще одно условие: частота генератора меньше частоты контура.

В некоторых случаях необходимо убрать резонансную частоту. Выполняется такая операция путем изменения необходимых характеристик электрической цепи «контурного генератора». Чаще всего в схеме используются конденсаторы с переменной емкостью, что дает возможность ее регулировки. Конденсатор настраивается изменением расстояния между его пластинами. Этот принцип очень удобен, так как нужен сердечник для изменения индуктивности катушки, которая будет скручена.

Однако радиоэлементы такого типа существуют. В них емкость является постоянной величиной, а индуктивность изменяется с помощью сердечника. Конструктивной особенностью последнего является обычный ферритовый болт, который вкручивается в пластиковый корпус. Кабель наматывается на последнюю.

Пример решения

Для устройства необходимо рассчитать контур с резонансной частотой 1 МГц.Можно воспользоваться описанными формулами, однако радиолюбители провели некоторые расчеты и предложили более упрощенный вариант: L=(159,1/f)^2/ C Для схемы можно взять примерное значение емкости плоского конденсатора равное 1000 пФ. Этот параметр указан на корпусе.

Также в маркировке может быть указано напряжение, на которое он рассчитан. Подставив все значения в формулу, можно найти индуктивность: L = (159,1/1)^2/1000 = 25 (мкГн). После этого нужно рассчитать количество витков N катушки при диаметре каркаса D по следующей зависимости: N = 32 * L/D^(½). Если принять, что D=5 мм (его можно взять из старых схем), то N=32*25/5^(½)=72 (виток). Однако за основу можно взять катушку с настроенным ферритовым сердечником со следующими параметрами:

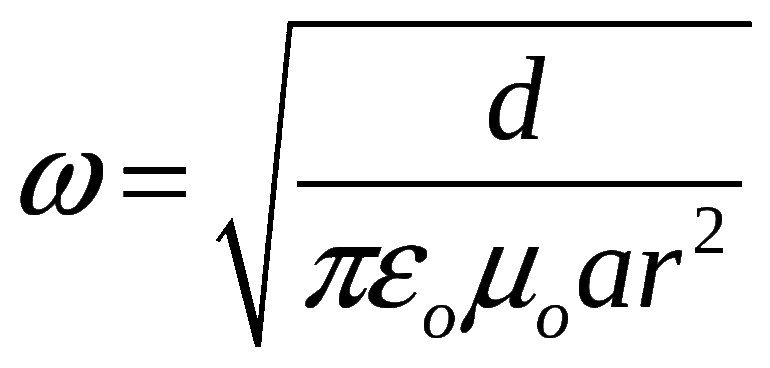
• длина — 13-15 мм;
• диаметр — 2,3-3,2 мм.

Можно использовать следующее соотношение: N=8,5*L^(½)=8,5*25^(½)=43 (поворот). Проволоку следует брать диаметром 0,1 мм. Этот показатель измеряется штангенциркулем.

Таким образом, колебательный контур представляет собой простейшую систему генерации электромагнитных колебаний, затухание которых зависит от резонансной частоты и добротности радиоэлемента.

Формула Томсона (резонанса) для последовательного колебательного контура

Если при резонансе мы имеем реактивное сопротивление катушки, равное реактивному сопротивлению конденсатора XL = XC, то мы можем уравнять их реактивные сопротивления и отсюда вычислить частоту, на которой произошел резонанс. Итак, реактивное сопротивление катушки выражается формулой:

Реактивное сопротивление конденсатора рассчитывается по формуле:

Приравниваем обе части и вычисляем F отсюда:

В этом случае мы получили формулу для резонансной частоты. Эту формулу также называют формулой Томсона, как вы понимаете, в честь ученого, который ее вывел.

Воспользуемся формулой Томсона для расчета резонансной частоты нашего последовательного колебательного контура. Для этого я буду использовать свой транзисторный измеритель RLC.

Измеряем индуктивность катушки:

И мы измеряем наши возможности:

Рассчитываем нашу резонансную частоту по формуле:

У меня 5,09 кГц.

С помощью подстройки частоты и осциллографа поймал резонанс на частоте 4,78 килогерц (написано в левом нижнем углу)

Исключим погрешность в 200 коп. Герц из-за погрешности измерений приборов. Как видите, формула Томпсона работает.

Последовательный колебательный контур обозначение на схеме

Последовательный колебательный контур представляет собой цепь, состоящую из катушки индуктивности и конденсатора, соединенных последовательно.

Идеальный последовательный колебательный контур

На схемах идеальный последовательный колебательный контур обозначается следующим образом:

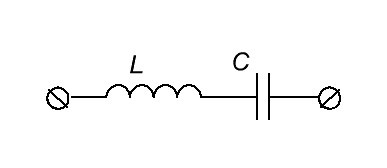
куда

L — индуктивность, Гн

С — емкость, Ф

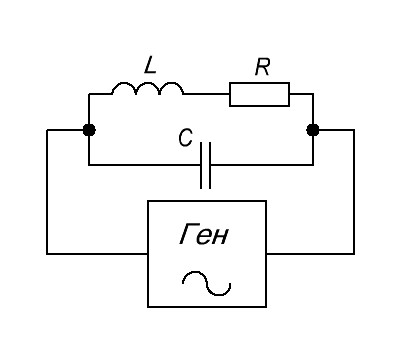
Реальный последовательный колебательный контур

Реальный колебательный контур имеет сопротивление потерь в конденсаторе и катушке. Это общее полное сопротивление потерь обозначается буквой R. В результате реальный последовательный колебательный контур будет выглядеть так:

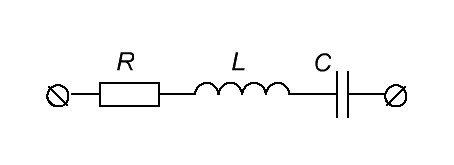
R — полное сопротивление потерь катушки и конденсатора

L — собственная индуктивность катушки

C — фактическая емкость конденсатора

Параллельный колебательный контур

Принцип работы параллельного колебательного контура

Подключим реальный параллельный колебательный контур к генератору частоты

Что будет, если подать на цепь ток с частотой ноль герц, то есть постоянный ток? Он будет плавно проходить через катушку и ограничиваться только сопротивлением потерь R самой катушки. Через конденсатор не будет протекать ток, потому что конденсатор не пропускает постоянный ток. Об этом я писал в статье Конденсатор в цепях постоянного и переменного тока.

Тогда добавим частоты. Итак, с увеличением частоты у нас есть конденсатор и катушка, которые начнут реагировать на электрический ток.

Реактивное сопротивление катушки выражается формулой

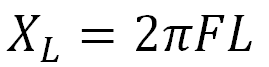
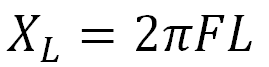
и конденсатор по формуле

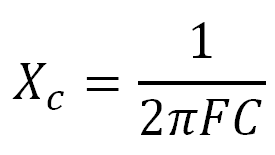
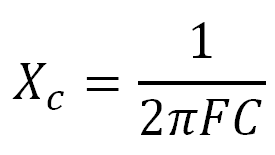
Если плавно увеличивать частоту, то из формул можно понять, что сначала при плавном увеличении частоты конденсатор будет давать большее сопротивление, чем дроссель. На некоторой частоте реактивные сопротивления катушки XL и конденсатора XC сравняются. Если увеличить частоту еще больше, катушка уже будет иметь большее сопротивление, чем конденсатор.

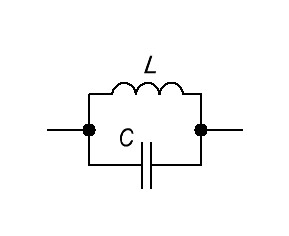
Идеальный колебательный контур

На схеме идеальный колебательный контур выглядит так:

куда

L — индуктивность, Генри

C — емкость, Фарад

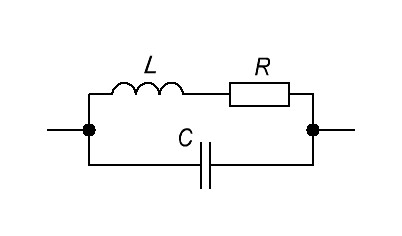
Реальный колебательный контур

На самом деле, наша катушка имеет приличное сопротивление останова, так как она намотана из провода, и конденсатор тоже имеет некоторое сопротивление останова. Емкостные потери очень малы и ими обычно пренебрегают. Поэтому оставляем только одно сопротивление потерь катушки R. Тогда схема реального колебательного контура примет следующий вид:

куда

R — сопротивление потерь в шлейфе, Ом

L — индуктивность, Генри

C — емкость, Фарад

Формула индуктивности

Расчет резонанса колебательного контура осуществляется на основе значений емкости и индуктивности. По общему правилу емкость конденсатора — величина постоянная, за исключением случаев, когда в перестраиваемых электрических цепях применяются переменные устройства. Коэффициент самоиндукции катушки зависит от многих факторов:

• Количество и расположение витков обмотки;
• Наличие или отсутствие ядра;
• Основной материал.

Общей формулы для определения индуктивности катушки колебательного контура не существует. Для расчетов используются формулы, соответствующие форме катушки. К сожалению, все формулы для определения качественного значения электрической цепи с подключенным индуктором допускают лишь приблизительные расчеты.

Индуктивные устройства различных типов

Важно! Для получения катушки с заданными параметрами необходимо принимать дополнительные меры, например регулировать коэффициент собственной индуктивности изменением длины сердечника или регулировкой расстояния между витками в однорядных катушках.

Общие сведения

Колебательный контур — это электрическая цепь, состоящая из конденсатора и катушки индуктивности, которая используется для генерации свободных электромагнитных колебаний в радиопередатчиках и приемниках. Это устройство используется в качестве различных фильтров (полосовых и режекторных). Для настройки сигналов в сторону увеличения или уменьшения амплитуды используется этот элемент радиуса. Основная функция схемы — частотная фильтрация.

Устройство получило широкое применение в военной сфере. Фильтры шумоподавления используются в радиолокационных станциях. Противник использует различные глушилки, блокирующие обнаружение цели. В состав оборудования входит специальное устройство, состоящее из обычной схемы, но с сердечником из специального сплава. Помехи «отфильтровываются» и оператор РЛС получает полную картину воздушной обстановки.

Устройство также может быть использовано для автоматизации. Например, самолеты включают в себя блок управления частотой. Основными его элементами являются два контура, настроенные всего на две частоты – 760 и 840 Гц, которые получают напряжение частотой 790 Гц от специального генератора. Последний излучает всего 395 Гц.Если частота отклоняется ниже номинального значения, то уменьшается реактивное сопротивление одного из контуров.

После этого срабатывает электроника блока и выдается сигнал на увеличение оборотов генератора. Когда значение частоты превышает номинальное значение, реактивное сопротивление другой цепи увеличивается. В результате этого срабатывает автоматика и поступает другой вид сигнала на снижение скорости генератора.

Резонанс напряжений

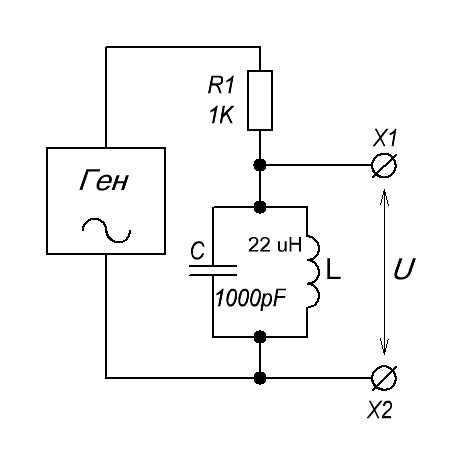
Возьмем другие параметры катушки и конденсатора и посмотрим, что происходит с радиоэлементами. Ведь нам предстоит все выяснить досконально ;-). Я беру дроссель индуктивностью 22 мкГн:

и конденсатор 1000 пФ

Из них собираю последовательный колебательный контур. Поэтому, чтобы поймать резонанс, я не буду добавлять резистор в схему. Я буду умнее.

Так как генератор частоты у меня китайский и маломощный, то при резонансе имеем в цепи только активное сопротивление потерь R. Суммарно мы все равно получаем небольшое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого на внутреннем сопротивлении генератора частоты падает приличное напряжение и падает амплитуда выходной частоты генератора. Я возьму минимальное значение этой амплитуды. Следовательно, это будет резонанс колебательного контура. Перегружать генератор нехорошо, но что поделаешь ради науки!

Что ж, приступим ;-). Сначала рассчитаем резонансную частоту по формуле Томсона. Для этого я открываю в интернете онлайн-калькулятор и быстро вычисляю эту частоту. У меня 1073 мегагерца.

Я улавливаю резонанс в генераторе частоты по его минимальным амплитудным значениям.

Хотя генератор частоты имеет колебание более 17 вольт! Вот тут и началось напряжение. И как видите, резонансная частота оказалась немного отличной от расчетной — 1109 мегагерц.

Это сигнал, который мы применяем к нашему последовательному колебательному контуру:

Как видите, мой генератор не может подавать большой ток в колебательный контур на резонансной частоте, поэтому сигнал получился даже немного искаженным на пиках.

Ну а теперь самое интересное. Измерим падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть так:

Смотрим напряжение на конденсаторе:

Амплитуда колебаний 20 вольт (5х4)! Где? Ведь на колебательный контур мы подаем синус с частотой 2 вольта!

Ок, может с осциллографом что-то случилось? Измеряем напряжение на катушке:

Люди! рекламный подарок! Они приложили 2 вольта от генератора и получили 20 вольт и на катушку и на конденсатор! Увеличение энергии в 10 раз! Успейте просто снять энергию с конденсатора или катушки!

Ну да ладно, раз такое дело… Беру лампочку на 12 вольт от мопеда и подключаю к конденсатору или катушке. Ведь лампочка вроде как по барабану на какой частоте работать и какой ток потреблять. Выставляю амплитуду так, чтобы катушка или конденсатор были где-то 20 Вольт, так как среднеквадратичное напряжение будет где-то 14 Вольт, и цепляю к ним по очереди лампочку:

Как видите, полный ноль. Лампочка не перегорит, так что любители бесплатной энергии бреются.) Вы помните, что мощность определяется произведением тока на напряжение? Напряжения вроде хватает, но силы тока, увы! Поэтому последовательный колебательный контур еще называют узкополосным (резонансным) усилителем напряжения, а не силовым!

Объяснение резонанса напряжения

При резонансе напряжение на катушке и на конденсаторе оказалось значительно больше того, которое мы приложили к колебательному контуру. В данном случае имеем в 10 раз больше. Почему напряжение на катушке при резонансе равно напряжению на конденсаторе? Это легко объяснимо. Так как в последовательном колебательном контуре катушка и преобразователь следуют друг за другом, следовательно, в цепи течет один и тот же ток.

В резонансе реактивное сопротивление катушки равно реактивному сопротивлению конденсатора. По правилу вывода получаем, что на катушке UL = IXL и на конденсаторе UC = IXC падает напряжение. А так как при резонансе у нас XL = XC, то и получаем, что UL = UC, потому что ток в цепи одинаков ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжения, так как напряжение на катушке при резонансной частоте равно напряжению на конденсаторе.

Как найти резонанс параллельного колебательного контура на практике

Хорошо, ближе к делу. Берем в руки паяльник и припаиваем параллельно катушку и конденсатор. Катушка 22uH и конденсатор 1000pF.

Таким образом, фактическая схема этой цепи будет такой:

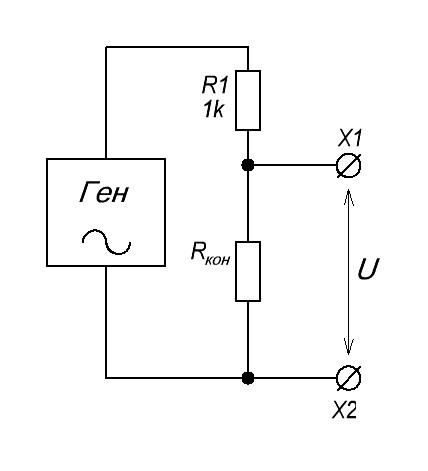
Чтобы показать все наглядно и понятно, добавим последовательно в схему резистор номиналом 1 КОм и соберем следующую схему:

На генераторе будем менять частоту, а с выводов Х1 и Х2 будем снимать напряжение и наблюдать на осциллографе.

Нетрудно догадаться, что наше сопротивление параллельного колебательного контура будет зависеть от частоты генератора, так как в этом колебательном контуре мы видим два радиоэлемента, реактивные сопротивления которых напрямую зависят от частоты, поэтому заменим колебательный контур на эквивалентное сопротивление генератора Rcon цепи.

Упрощенная схема будет выглядеть так:

Интересно, как выглядит эта цепь. Это делитель напряжения? Точно! Итак, мы помним правило делителя напряжения: меньше падает напряжение при меньшем сопротивлении, больше падает напряжение при большем сопротивлении. Какой вывод можно сделать относительно нашего колебательного контура? Да все просто: на резонансной частоте сопротивление Rcon будет максимальным, в результате чего на этом резисторе будет «падать» большее напряжение.

Приступим к нашему опыту. Поднимаем частоту в генераторе, начиная с самых маленьких частот.

200 герц

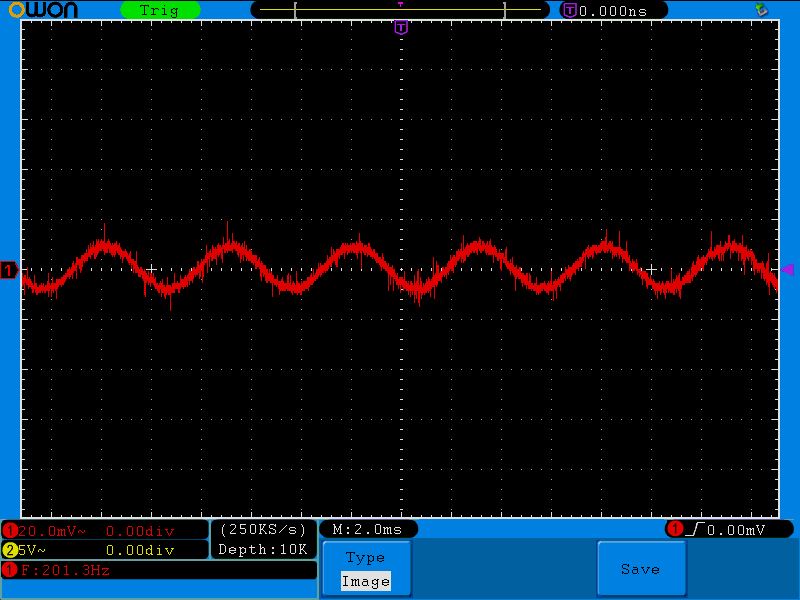
Как видим, в колебательном контуре «падает» небольшое напряжение, а значит, по правилу делителя напряжения теперь можно сказать, что контур имеет малое сопротивление Rкон

Добавление частоты. 11,4 кГц

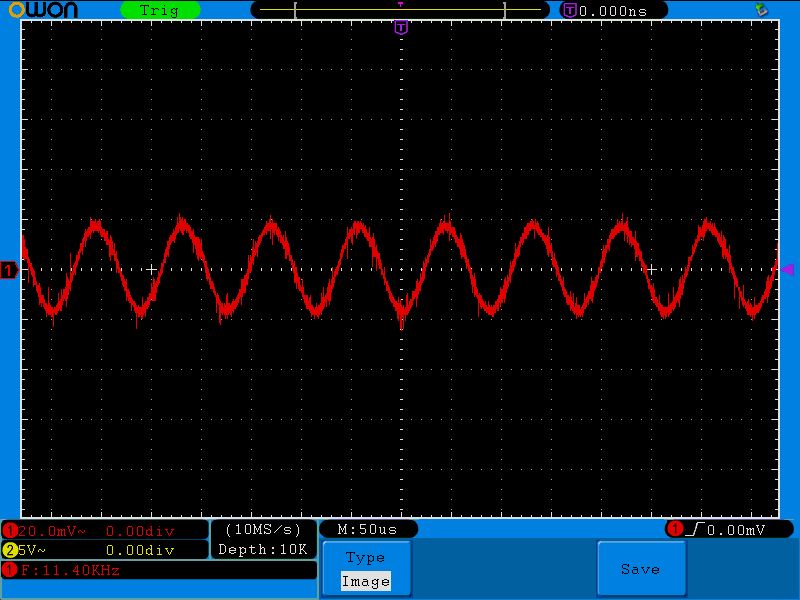
Как видите, напряжение в цепи увеличилось. Это означает, что сопротивление колебательного контура увеличилось.

Добавьте больше частоты. 50 кГц

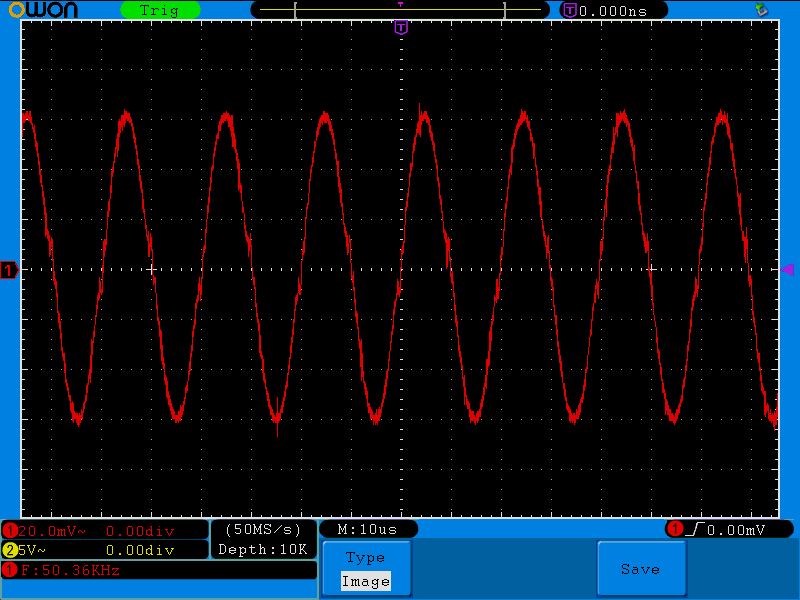
Обратите внимание, что напряжение в цепи увеличилось еще больше. Затем его сопротивление возросло еще больше.

723 кГц

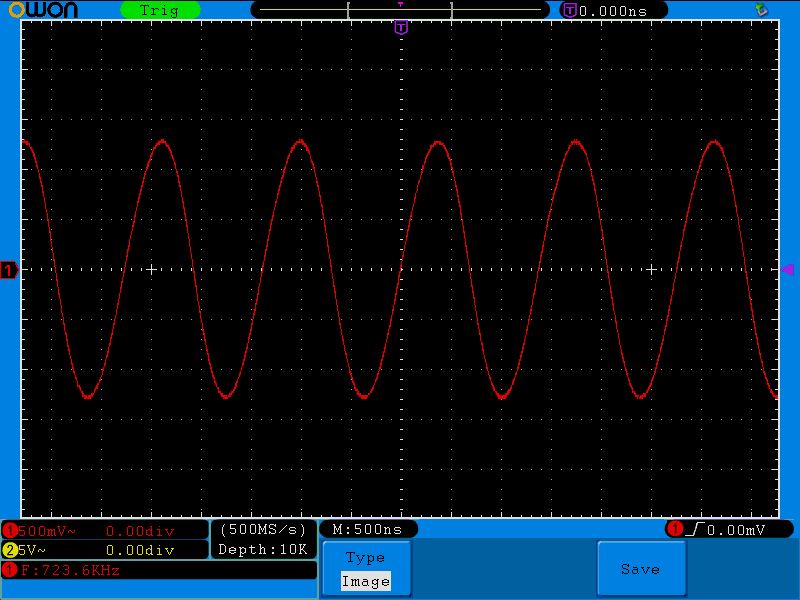
Обратите внимание на цену деления квадрата по вертикали по сравнению с предыдущим опытом. Было 20 мВ на квадрат, а сейчас 500 мВ на квадрат. Напряжение возрастало, так как сопротивление колебательного контура становилось еще выше.

И вот я поймал частоту, при которой было получено максимальное напряжение в колебательном контуре. Обратите внимание на значение деления по вертикали. Он равен двум вольтам.

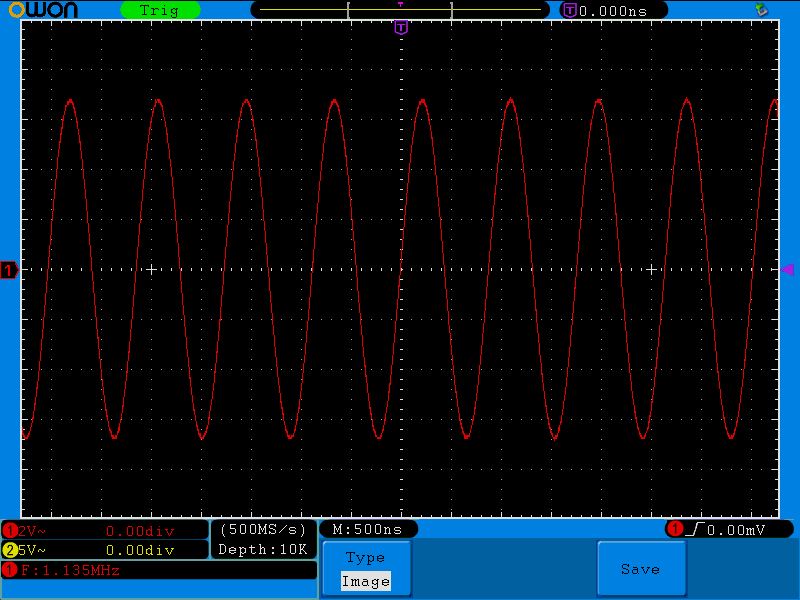
Дальнейшее увеличение частоты приводит к тому, что напряжение начинает падать:

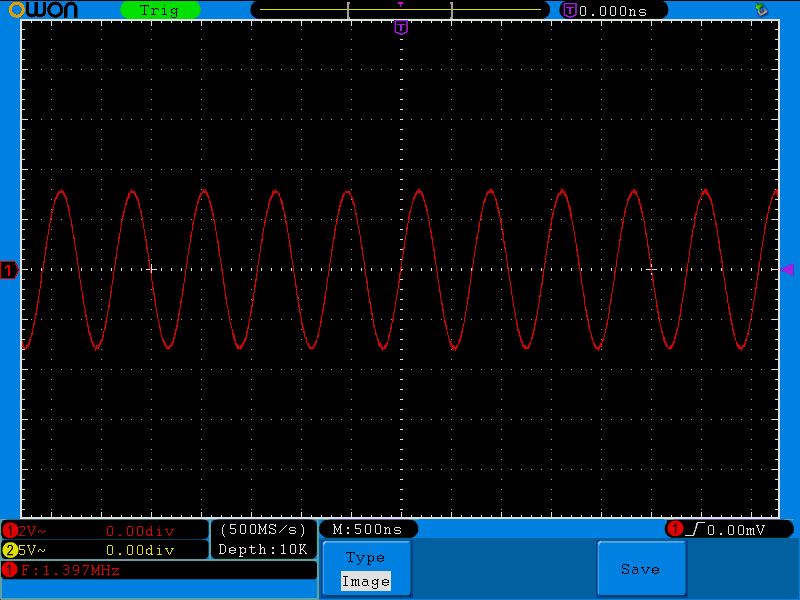
Снова прибавляем частоту и видим, что напряжение стало еще ниже:

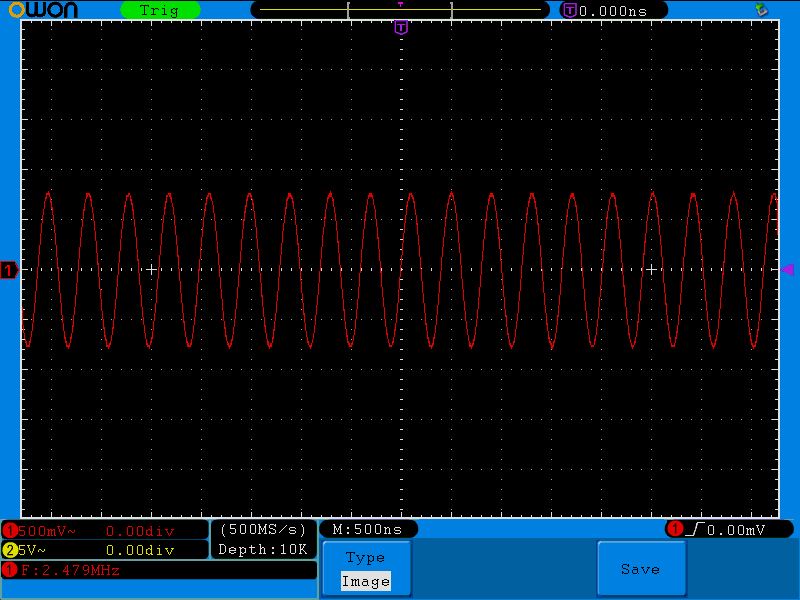
Что происходит на резонансной частоте в параллельном колебательном контуре

Давайте внимательнее посмотрим на этот сигнал, когда у нас было максимальное напряжение в цепи.

Что здесь случилось?

Так как на этой частоте имел место подъем напряжения, следовательно, на этой частоте параллельный колебательный контур имел наибольшее сопротивление Rкон. На этой частоте XL = XC. Затем по мере увеличения частоты сопротивление цепи снова падало. Это и есть то самое резонансное сопротивление цепи, которое выражается формулой:

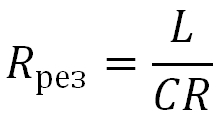
Резонанс токов

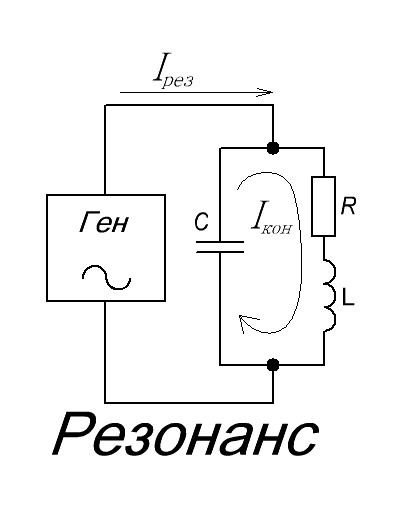
Итак, допустим, мы привели наш колебательный контур в резонанс:

Каким будет резонансный ток Ires? Рассчитываем по закону Ома:

Ires = Ugen / Rres, где Rres = L/CR.

Но самое смешное, что при резонансе в цепи у нас появляется своя иконка тока цепи, которая не выходит за пределы контура и остается только в самой цепи. Поскольку у меня проблемы с математикой, я не буду приводить различные математические расчеты с производными и комплексными числами или объяснять, откуда берется контурный ток при резонансе. Вот почему резонанс параллельного колебательного контура называют токовым резонансом.

Как определяется добротность колебательного контура?

Качество колебательного контура определяется добротностью Q, которая является основным параметром контура. Добротность цепи – это отношение реактивной мощности к потерям мощности в цепи. Реактивная мощность определяется по формуле: P = I 2 (ωL –).

Добротность параллельного колебательного контура

Кстати, этот контурный ток будет намного больше, чем ток, проходящий через контур. И знаете, сколько раз? Правильно, Q раз. Р — это добротность! В параллельном колебательном контуре показывает, во сколько раз сила тока в цепи Ikon больше силы тока в общей цепи Ires

Или формула:

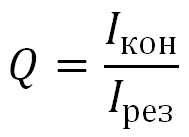
Если сюда же положить и устойчивость к потерям, то формула примет следующий вид:

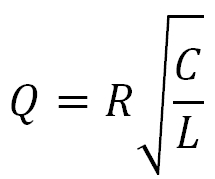
куда

Q — добротность

R — сопротивление потерь в катушке, Ом

С — емкость, Ф

L — индуктивность, Гн

Применение параллельного колебательного контура

Параллельный колебательный контур применяется в радиоприемной аппаратуре, где необходимо выбирать частоту станции. Также с помощью колебательного контура можно строить различные резонансные фильтры.